链表长度计算方法:详解如何高效获取链表长度
链表是什么?
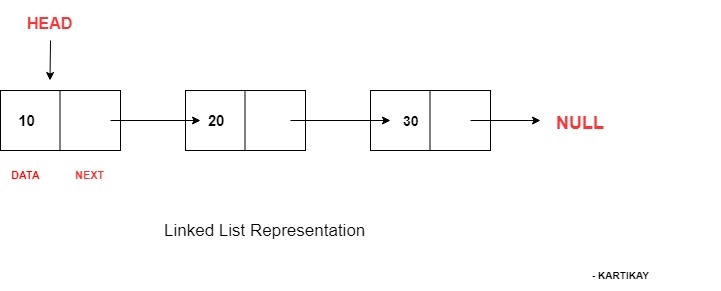
- 链表是一种用于存储数据集合的线性数据结构
- 连续的元素通过指针连接
- 最后一个元素指向NULL(空值)
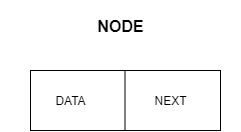
- 每个元素是一个独立的对象,称为节点(Node)
- 链表中的每个节点包含两部分:数据和指向下一个节点的引用
如何找到链表的长度?
找到链表的长度有两种方法。
- 迭代方法
- 递归方法
使用迭代方法计算链表的长度
我们将使用链表遍历来找到链表的长度。
- 头节点(Head)指向链表的第一个节点
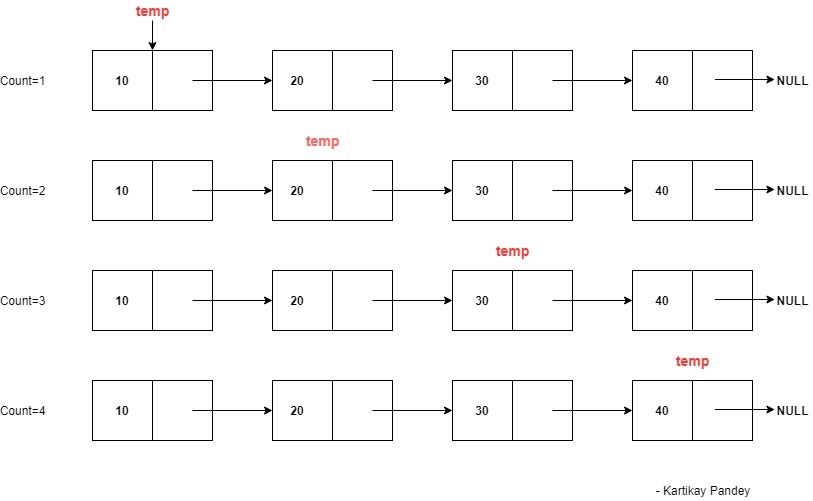
- 将计数变量(count)初始化为0
- 将临时变量(temp)初始化为头节点(Head)
- 每访问一个节点,计数变量的值就增加1
- 当到达空值(null)时停止过程
- 不要改变头节点的引用
用Java编码
package com.Olivia.ds;
public class MyLinkedList {
public class Node {
int data;
Node next;
}
public Node head;
public Node tail;
public int size;
public int getFirst() throws Exception {
if (this.size == 0) {
throw new Exception("链表为空");
}
return this.head.data;
}
public int getLast() throws Exception {
if (this.size == 0) {
throw new Exception("链表为空");
}
return this.tail.data;
}
public void display() {
Node temp = this.head;
while (temp != null) {
System.out.println(temp.data + " ");
temp = temp.next;
}
}
public void addFirst(int item) {
Node nn = new Node();
nn.data = item;
if (this.size == 0) {
this.head = nn;
this.tail = nn;
this.size = this.size + 1;
} else {
nn.next = this.head;
this.head = nn;
this.size = this.size + 1;
}
}
public int length() {
Node temp = this.head;
int count = 0;
while (temp != null) {
count++;
temp = temp.next;
}
return count;
}
public static void main(String[] args) {
MyLinkedList ll = new MyLinkedList();
ll.addFirst(10);
ll.addFirst(20);
ll.addFirst(30);
ll.addFirst(40);
ll.addFirst(50);
System.out.println("链表长度为 " + ll.length());
}
}
在C语言中编码
#include <stdio.h>
#include <stdlib.h>
/* 链表节点的结构 */
struct node {
int data;
struct node *next;
} *head;
void initialize(){
head = NULL;
}
/*
在单链表前面插入一个节点
*/
void insert(int num) {
/* 创建一个新的链表节点 */
struct node* newNode = (struct node*) malloc(sizeof(struct node));
newNode->data = num;
/* 新节点的下一个指针将指向链表的头节点 */
newNode->next = head;
/* 使新节点成为链表的新头节点 */
head = newNode;
printf("插入的元素 : %d\n", num);
}
int getLength(struct node *head){
int length =0;
while(head != NULL){
head = head->next;
length++;
}
return length;
}
/*
从头节点到尾节点打印链表
*/
void printLinkedList(struct node *nodePtr) {
while (nodePtr != NULL) {
printf("%d", nodePtr->data);
nodePtr = nodePtr->next;
if(nodePtr != NULL)
printf("-->");
}
}
int main() {
initialize();
/* 创建一个链表 */
insert(8);
insert(3);
insert(2);
insert(7);
insert(9);
printf("\n链表\n");
printLinkedList(head);
printf("\n链表长度 : %d", getLength(head));
return 0;
}
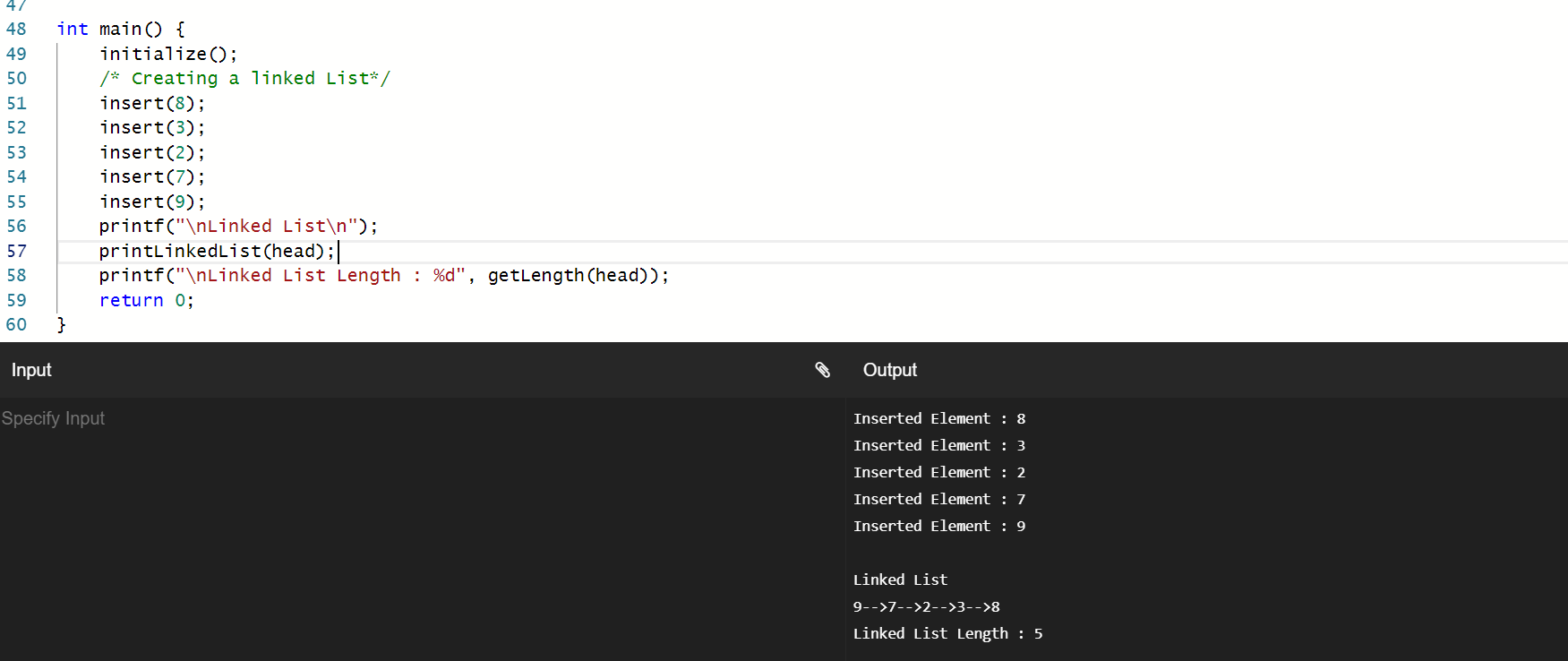
结果
使用递归解决方案计算链表的长度
基础情况:
- 最后一个节点指向空值(Null)
- 返回0
递归情况:
- 在每一步,将当前节点的值更新为下一个节点
- 调用 = 1+fun(curr.next)
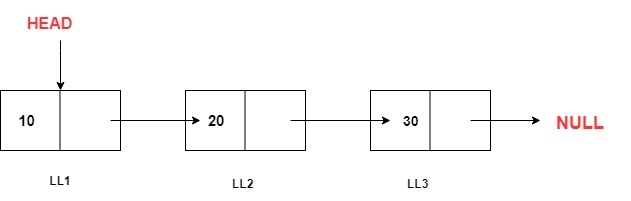
在链表中有3个元素:LL1、LL2和LL3。当进行递归调用时,我们将观察内存堆栈中发生的情况。内存堆栈:
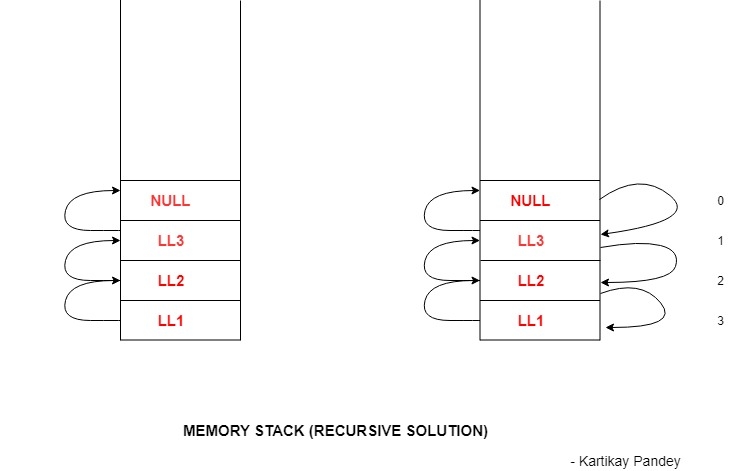
主函数调用LL1,LL1调用LL2,LL2调用LL3,LL3调用空值。当达到空值时,我们从这里返回。0被返回给LL3,LL3向LL2返回1,LL2向LL1返回2,最后LL1向主函数返回3。
使用Java进行编码
Java实现递归方法计算链表长度
下面是一个完整的Java实现,展示了如何使用递归方法计算链表的长度。我们首先定义了一个链表类,其中包含节点类、头节点、尾节点和大小属性。
package com.Olivia.ds;
public class MyLinkedList {
public class Node {
int data;
Node next;
}
public Node head;
public Node tail;
public int size;
public int getfirst() throws Exception {
if (this.size == 0) {
throw new Exception("链表为空");
}
return this.head.data;
}
public int RemoveFirst() throws Exception {
if (this.size == 0) {
throw new Exception("链表为空");
}
Node temp = this.head;
if (this.size == 1) {
this.head = null;
this.tail = null;
size = 0;
} else {
this.head = this.head.next;
this.size--;
}
return temp.data;
}
public void addFirst(int item) {
Node nn = new Node();
nn.data = item;
if (this.size == 0) {
this.head = nn;
this.tail = nn;
this.size = this.size + 1;
} else {
nn.next = this.head;
this.head = nn;
this.size = this.size + 1;
}
}
public int lengthUsingRecursiveApproach (){
return lengthUsingRecursiveApproach(this.head);
}
private int lengthUsingRecursiveApproach(Node curr) {
// 自动生成的方法存根
if (curr == null) {
return 0;
}
return 1 + lengthUsingRecursiveApproach (curr.next);
}
public static void main(String[] args) {
MyLinkedList ll = new MyLinkedList();
// 向链表中插入元素
ll.addFirst(10);
ll.addFirst(20);
ll.addFirst(30);
ll.addFirst(40);
ll.addFirst(50);
// 链表长度
System.out.println("递归方法计算链表长度 " + ll.lengthUsingRecursiveApproach(ll.head));
}
}
C语言实现递归方法计算链表长度
接下来,我们看看如何在C语言中实现递归方法来计算链表的长度。C语言实现需要手动管理内存,使用malloc函数为节点分配内存空间。
#include <stdio.h>
struct Node
{
int data;
struct Node* next;
};
void push(struct Node** head_ref, int new_data)
{
struct Node* new_node = (struct Node*) malloc(sizeof(struct Node));
new_node->data = new_data;
/* 将新节点链接到旧列表 */
new_node->next = (*head_ref);
(*head_ref) = new_node;
}
int getCount(struct Node* head)
{
// 基本情况
if (head == NULL)
return 0;
return 1 + getCount(head->next);
}
int main()
{
struct Node* head = NULL;
push(&head, 1);
push(&head, 3);
push(&head, 1);
push(&head, 2);
push(&head, 1);
printf("节点数量为 %d", getCount(head));
return 0;
}
输出结果
时间复杂度分析
在递归和迭代解决方案中,时间复杂度均为O(N),因为我们只需要进行一次遍历来得知链表的长度。递归方法的优点是代码简洁,但缺点是可能会因为递归深度过大而导致栈溢出,特别是对于非常长的链表。在实际应用中,应根据链表的可能长度和系统资源情况选择合适的方法。

