小数背包问题C++实现:贪心算法详解与代码示例
在这篇文章中,我们将学习如何使用C++解决分数背包问题。我们将首先看一下问题陈述,然后再转向解决方案。这个问题是众多经典问题中的一个。它与其兄弟问题0-1背包和0-N背包相当不同。这是一种贪婪算法,而其他两种是动态规划算法。
什么是分数背包问题?
你被给予某些物品的重量和价格清单,以及一个特定容量的袋子/背包,称为W。你的任务是以这样的方式填满这个袋子,使得你放入袋子的所有物品的总价格对于所有配置来说都是最大的。而且你可以整个地或者部分地收集任何物品。
分数背包算法
好的,让我们来看一下解决这个问题的算法。由于我们将实施一种贪婪算法来解决这个问题,下面是贪婪算法的简要描述。
什么是贪婪算法?
在这些算法中,我们的目标是在每一步中实现局部最大/最小值,以便最终达到全局最大/最小值。也就是说,我们在解决每个子问题时都要最大化/最小化答案,这将带领我们找到整体问题的最大/最小答案。
注意:你即将做出的贪婪选择必须是一个安全的行动。
安全着法:若存在与初始着法相应的可靠的最优解,该着法即为安全着法。
与贪婪算法合作的策略
以下是你应该遵循的步骤,以开发完美的贪婪算法。
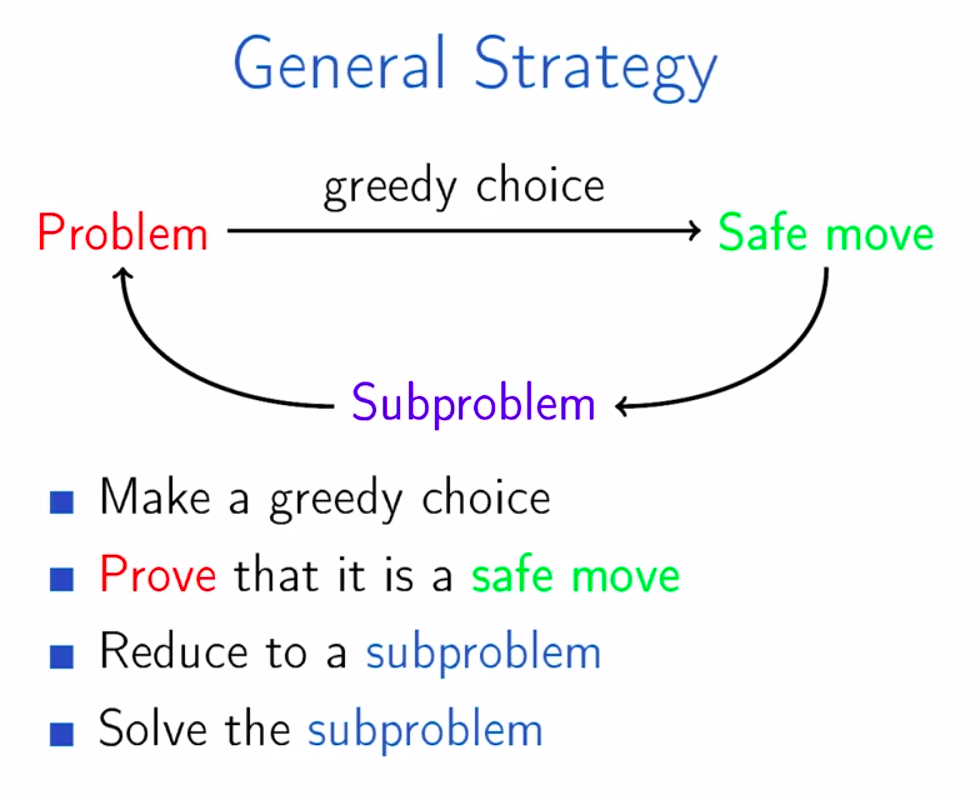
- 做出贪婪选择
- 证明它是一个安全着法,这样你就不会在编写代码后才发现它不是一个可行的选择。这一特定步骤是贪婪算法中最重要的步骤。
- 简化为更小的问题
- 解决所有更小的问题。
伪代码
现在我们将逐步学习背包算法。
- 按照价值/重量比的降序对物品进行排序。仅这一步就将最佳物品选择的时间复杂度从O(N)降低到O(log2N)。
- 现在我们通过运行一个从i = 0到i = N的for循环来开始选择物品。
- 引理:存在一个最优解,该解尽可能多地使用具有每单位重量最大价值的物品。
证明:尝试通过不同的选择标准来填充背包,你将总是得到小于最大可能值的总价值。 - 现在,如果具有最大价值/重量比的物品的大小适合背包,则全部取用。否则,取用它的最大可能分数。
- 通过所取物品的重量来减少背包的容量。
如果整个物品被取用,则:capacity = capacity – weight[this_item]。
否则,容量变为0,因为背包变满了。 - 将所取物品的分数价值添加到总价值中。
如果整个物品被取用:total_value += value[this_item]
否则,value += fraction_of_weight_taken * value[this_item]。 - 如果容量变为0,则跳出循环。
伪代码的总体结构变为:

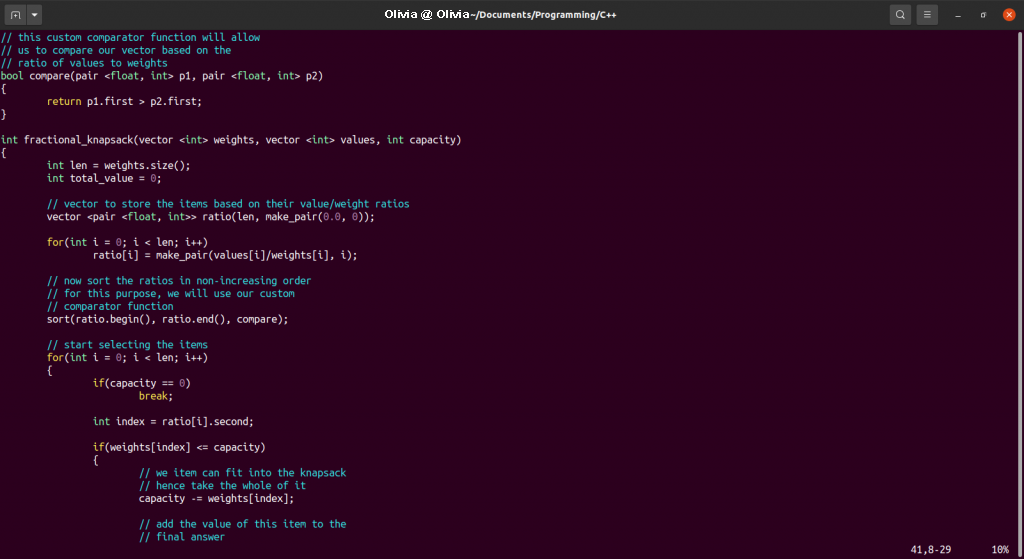
展示分数背包问题的C++程序
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
// 这个自定义比较函数将允许
// 我们根据价值与重量的比率
// 来比较向量
bool compare(pair <float, int> p1, pair <float, int> p2)
{
return p1.first > p2.first;
}
int fractional_knapsack(vector <int> weights, vector <int> values, int capacity)
{
int len = weights.size();
int total_value = 0;
// 用于根据物品的价值/重量比率存储物品的向量
vector <pair <float, int>> ratio(len, make_pair(0.0, 0));
for(int i = 0; i < len; i++)
ratio[i] = make_pair(values[i]/weights[i], i);
// 现在按非递增顺序排序这些比率
// 为此,我们将使用自定义的
// 比较函数
sort(ratio.begin(), ratio.end(), compare);
// 开始选择物品
for(int i = 0; i < len; i++)
{
if(capacity == 0)
break;
int index = ratio[i].second;
if(weights[index] <= capacity)
{
// 物品可以放入背包
// 因此取整个物品
capacity -= weights[index];
// 将该物品的价值添加到
// 最终答案中
total_value += values[index];
}
else
{
// 这个物品不能完全放入背包
// 因此我们取它的一部分
int value_to_consider = values[index] * (float(capacity)/float(weights[index]));
total_value += value_to_consider;
capacity = 0;
}
}
return total_value;
}
int main()
{
cout << "请输入物品的重量,输入-1停止" << endl;
vector <int> weights;
while(true)
{
int weight;
cin >> weight;
if(weight == -1)
break;
weights.push_back(weight);
}
cout << "请输入每个物品的价值,输入-1停止" << endl;
vector <int> values;
while(true)
{
int value;
cin >> value;
if(value == -1)
break;
values.push_back(value);
}
cout << "请输入背包的容量" << endl;
int capacity;
cin >> capacity;
cout << "根据当前列表,可能的最大价值是: " << fractional_knapsack(weights, values, capacity) << endl;
}
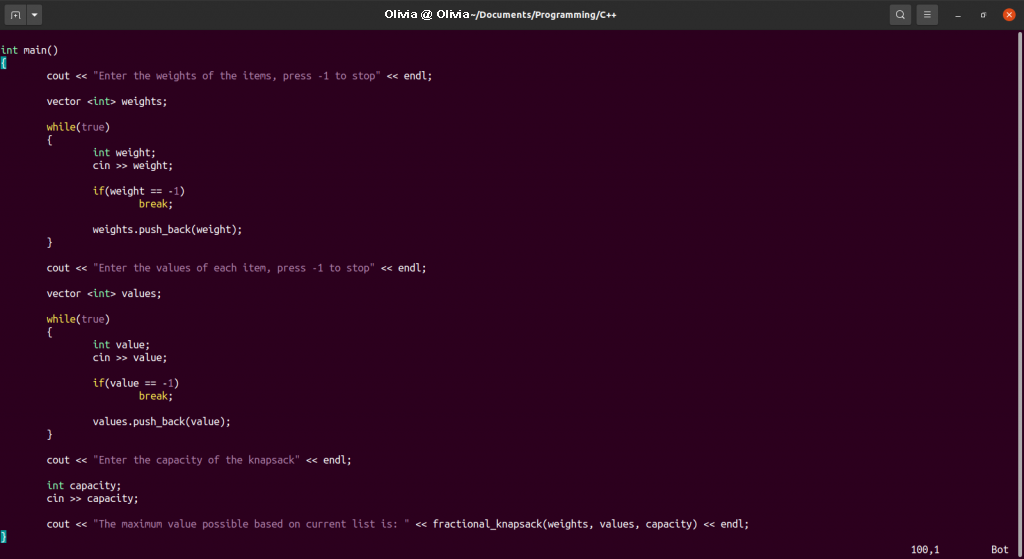
产出结果
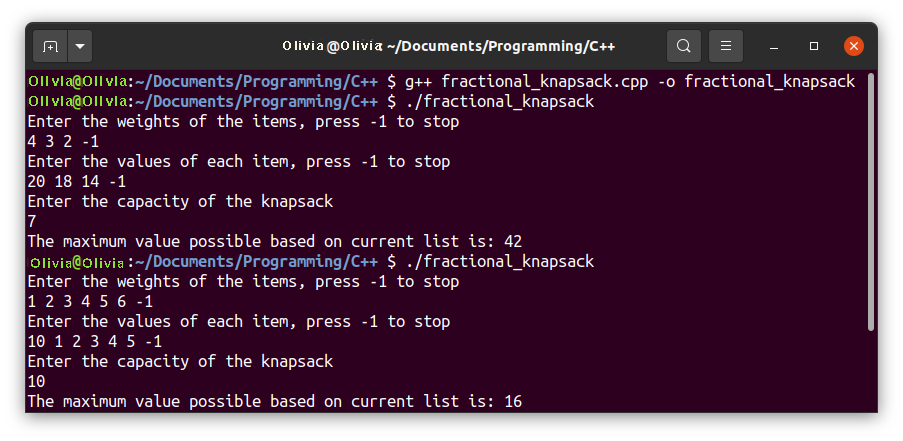
结论
分数背包问题是一种贪心算法,在本文中,我们讨论了其实现。我们简要介绍了贪心算法的基本概念,然后详细讨论了分数背包算法的伪代码。我们证明了贪心选择的正确性,最后通过一个C++程序来演示这个解决方案。该算法的总时间复杂度为:O(Nlog2N)。感谢您的阅读!
延伸阅读
如果您想深入了解背包问题和其他贪心算法的相关内容,可以参考以下资源:
贪心算法是一种常用于解决优化问题的算法范式。它通过在每个决策点都选择当前最优的选项,期望最终得到全局最优解。
以下是对《0/1背包问题》维基百科页面的中文释义:
0/1背包问题,也称为背包问题,是一个组合优化问题。其目标是从给定的物品集合中选择若干物品放入容量有限的背包中,使得所选物品的总价值最大,同时不超过背包的容量限制。

