Python中ReLu激活函数详解:原理、实现与在神经网络中的应用
ReLU或修正线性激活函数是深度学习领域中最常见的激活函数选择。ReLU在提供最先进的结果的同时,计算效率也非常高。
ReLU激活函数的基本概念是:
如果输入为负数则返回0,否则返回输入值本身。我们可以用数学方式表示它,如下所示:
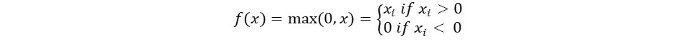
ReLU的伪代码如下所示:
# 如果输入大于0
if input > 0:
# 返回输入值
return input
else:
# 否则返回0
return 0
在本教程中,我们将学习如何实现自己的ReLU函数,了解它的一些缺点,并学习一个更好的ReLU版本。
推荐阅读:《机器学习的线性代数》第一篇
我们开始吧!
在Python中实现ReLU函数
让我们用Python编写自己的ReLU实现。我们将使用内置的max函数来实现它。
ReLU的代码如下:
# 定义ReLU函数
def relu(x):
# 返回0和x中的较大值
return max(0.0, x)
为了测试这个函数,让我们在几个输入上运行它。
# 测试正数
x = 1.0
print('对(%.1f)应用ReLU得到%.1f' % (x, relu(x)))
# 测试负数
x = -10.0
print('对(%.1f)应用ReLU得到%.1f' % (x, relu(x)))
# 测试零
x = 0.0
print('对(%.1f)应用ReLU得到%.1f' % (x, relu(x)))
# 测试更大的正数
x = 15.0
print('对(%.1f)应用ReLU得到%.1f' % (x, relu(x)))
# 测试更小的负数
x = -20.0
print('对(%.1f)应用ReLU得到%.1f' % (x, relu(x)))
完整代码
ReLU函数的Python实现
以下是ReLU函数的完整Python代码实现:
def relu(x):
return max(0.0, x)
x = 1.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -10.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 0.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = 15.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
x = -20.0
print('Applying Relu on (%.1f) gives %.1f' % (x, relu(x)))
代码输出结果
上述代码的输出结果如下:
Applying Relu on (1.0) gives 1.0
Applying Relu on (-10.0) gives 0.0
Applying Relu on (0.0) gives 0.0
Applying Relu on (15.0) gives 15.0
Applying Relu on (-20.0) gives 0.0
ReLU函数的梯度
让我们来看一下ReLU函数的梯度(导数)。对ReLU函数求导后,我们会得到以下分段函数:
f'(x) = 1, x>=0
= 0, x<0
从上面的导数公式可以看出,对于小于零的x值,ReLU函数的斜率为0。这意味着在神经网络训练过程中,某些神经元的权重和偏置将不会被更新,这可能导致”神经元死亡”的问题,从而影响模型的训练效果。
为了克服这个问题,研究者们提出了泄漏线性整流函数(Leaky ReLU)。接下来让我们详细了解一下Leaky ReLU函数。
泄漏ReLU函数(Leaky ReLU)
泄漏ReLU函数是常规ReLU函数的改进版本。为了解决负值梯度为零的问题,泄漏ReLU对负输入提供了一个极小的线性斜率,而不是直接将其设置为零。
从数学上讲,我们可以将Leaky ReLU表示为:
f(x)= 0.01x, x<0
= x, x>=0
从数学角度来看,Leaky ReLU函数可以表示为:
- f(x) = αx, 当 x < 0 时
- f(x) = x, 当 x ≥ 0 时
这里的α是一个小常数,通常取值为0.01,就像我们在上面的公式中所使用的那样。这个小的斜率确保了对于负输入,神经元仍然会有一个非零的梯度,从而避免了”神经元死亡”的问题。
以图形形式表示,Leaky ReLU函数如下所示:
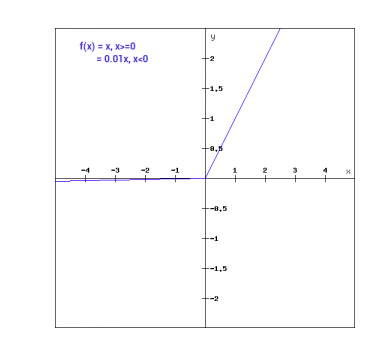
Leaky ReLU的梯度
Leaky ReLU函数的梯度(导数)如下:
f'(x) = 1, x>=0
= 0.01, x<0
从导数公式可以看出,Leaky ReLU在负值区域也有一个非零的梯度(0.01),这使得即使在负输入的情况下,神经元也能够进行权重更新,从而避免了传统ReLU函数中的”神经元死亡”问题。
让我们来计算Leaky ReLu函数的梯度。梯度可以得出为:
f'(x) = 1, x>=0
= 0.01, x<0
在这种情况下,负输入的梯度不为零。这意味着所有的神经元都将被更新。
在Python中实现Leaky ReLu
下面给出了Leaky ReLu的实现方法:
def leaky_relu(x):
if x>0 :
return x
else :
return 0.01*x
让我们现场尝试一下输入。
x = 1.0
print('在(%.1f)上应用Leaky ReLu得到%.1f' % (x, leaky_relu(x)))
x = -10.0
print('在(%.1f)上应用Leaky ReLu得到%.1f' % (x, leaky_relu(x)))
x = 0.0
print('在(%.1f)上应用Leaky ReLu得到%.1f' % (x, leaky_relu(x)))
x = 15.0
print('在(%.1f)上应用Leaky ReLu得到%.1f' % (x, leaky_relu(x)))
x = -20.0
print('在(%.1f)上应用Leaky ReLu得到%.1f' % (x, leaky_relu(x)))
完整的代码
下面是Leaky ReLu的完整代码:
def leaky_relu(x):
if x>0 :
return x
else :
return 0.01*x
x = 1.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -10.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 0.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = 15.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
x = -20.0
print('Applying Leaky Relu on (%.1f) gives %.1f' % (x, leaky_relu(x)))
輸出:
Applying Leaky Relu on (1.0) gives 1.0
Applying Leaky Relu on (-10.0) gives -0.1
Applying Leaky Relu on (0.0) gives 0.0
Applying Leaky Relu on (15.0) gives 15.0
Applying Leaky Relu on (-20.0) gives -0.2

