深入理解C/C++字典树：原理、实现与优化技巧

2 年 ago
韵, 科
9 minutes

这是文章《C/C++中的字典树数据结构》的第1部分（共7部分）。

字典树（Trie）数据结构作为一个动态数组的容器。在本文章中，我们将看一下如何在C/C++中实现一个字典树（Trie）。

这是基于树数据结构的，但不一定存储键。在这里，每个节点只有一个值，该值是根据位置定义的。

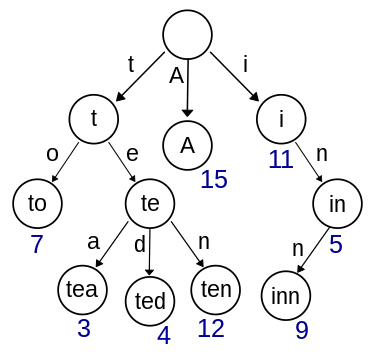
所以，每个节点的值表示前缀，因为它是经过一系列匹配后从根节点出发的点。

我们把这样的匹配称为前缀匹配。因此，我们可以使用字典树（Trie）来存储字典中的词语！

例如，在上图中，根节点为空，因此每个字符串都匹配根节点。节点7匹配了一个以”to”为前缀的字符串，而节点3匹配了一个以”tea”为前缀的字符串。

在这里，键只存储在叶子节点的位置上，因为前缀匹配会停在任何叶子节点。因此，任何非叶子节点都不存储整个字符串，而只存储前缀匹配的字符。

出于这些原因，字典树也被称为前缀树。现在让我们从程序员的角度来理解如何实现这种数据结构。

在C/C++中实现字典树数据结构

让我们首先写下字典树结构。字典树节点主要有两个组成部分。

  • 它的子节点
  • 一个标记，用于指示叶子节点

然而，由于我们还将打印字典树，如果我们能够在数据部分中存储一个附加属性，那将更容易。

那么让我们来定义TrieNode的结构。在这里，由于我只会存储小写字母，我将将其实现为一棵26叉树。因此，每个节点将有指向26个子节点的指针。

// 每个节点的子节点数量
// 我们将构建一个N叉树并使其成为字典树
// 由于我们有26个英文字母，每个节点需要26个子节点
#define N 26

typedef struct TrieNode TrieNode;

struct TrieNode {
    // 字典树节点结构
    // 每个节点从根节点开始有N个子节点
    // 还有一个标记来检查它是否是叶子节点
    char data; // 仅用于打印目的
    TrieNode* children[N];
    int is_leaf;
};

既然我们已经定义了结构，让我们编写函数来初始化字典树节点，并且还要释放其指针。

TrieNode* make_trienode(char data) {
    // 为字典树节点分配内存
    TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
    for (int i=0; i<N; i++)
        node->children[i] = NULL;
    node->is_leaf = 0;
    node->data = data;
    return node;
}

void free_trienode(TrieNode* node) {
    // 释放字典树节点序列
    for(int i=0; i<N; i++) {
        if (node->children[i] != NULL) {
            free_trienode(node->children[i]);
        }
        else {
            continue;
        }
    }
    free(node);
}

将一个词插入到字典树数据结构中

这是文章《C/C++中的字典树数据结构》的第2部分（共7部分）。

现在我们将编写insert_trie()函数，该函数接收根节点（最顶层节点）的指针，并将一个单词插入到字典树（Trie）中。

插入过程很简单。它逐个字符地迭代单词，并评估其相对位置。

例如，字符’b’的位置是1，所以它将成为第二个子元素。

for (int i=0; word[i] != '\0'; i++) {
    // 获取字母表中的相对位置
    int idx = (int) word[i] - 'a';
    if (temp->children[idx] == NULL) {
        // 如果对应的子节点不存在，
        // 就创建该子节点！
        temp->children[idx] = make_trienode(word[i]);
    }
    else {
        // 不做任何操作。该节点已存在
    }

我们将逐个字符匹配前缀，并在必要时简单地初始化一个节点。

否则，我们只需要一直沿着链条向下移动，直到匹配所有字符。

temp = temp->children[idx];

最后，我们将插入所有不匹配的字符，并将更新后的字典树（Trie）返回。

TrieNode* insert_trie(TrieNode* root, char* word) {
    // 将单词插入到字典树中
    // 假设：单词只包含小写字母
    TrieNode* temp = root;

    for (int i=0; word[i] != '\0'; i++) {
        // 获取字母表中的相对位置
        int idx = (int) word[i] - 'a';
        if (temp->children[idx] == NULL) {
            // 如果对应的子节点不存在，
            // 就创建该子节点！
            temp->children[idx] = make_trienode(word[i]);
        }
        else {
            // 不做任何操作。该节点已存在
        }
        // 向下移动一层，到idx引用的子节点
        // 因为我们有前缀匹配
        temp = temp->children[idx];
    }
    // 在单词的末尾，将此节点标记为叶子节点
    temp->is_leaf = 1;
    return root;
}

在字典树（Trie）中搜索单词

C/C++中的字典树数据结构 – 第3部分（共7部分）

现在我们已经实现了字典树(Trie)的插入操作，接下来让我们看一下如何搜索给定的模式。

我们将尝试逐个字符匹配字符串，采用与前面相同的前缀匹配策略。

如果我们已经到达链的末尾，但仍然没有找到匹配项，这意味着字符串不存在，因为没有完成完整的前缀匹配。

为了使搜索正确返回，我们的模式必须完全匹配，并且在匹配完成后，我们必须到达一个叶节点。

int search_trie(TrieNode* root, char* word)
{
    // 在字典树中搜索单词
    TrieNode* temp = root;

    for(int i=0; word[i]!='\0'; i++)
    {
        int position = word[i] - 'a';
        if (temp->children[position] == NULL)
            return 0;
        temp = temp->children[position];
    }
    if (temp != NULL && temp->is_leaf == 1)
        return 1;
    return 0;
}

好的，我们已经完成了插入和搜索的步骤。

为了测试这些功能，我们首先编写一个print_trie()函数，用于打印每个节点的数据。

void print_trie(TrieNode* root) {
    // 打印字典树的节点
    if (!root)
        return;
    TrieNode* temp = root;
    printf("%c -> ", temp->data);
    for (int i=0; i<N; i++) {
        print_trie(temp->children[i]); 
    }
}

既然我们已经实现了这些功能，让我们运行完整的程序来检查它是否正常工作。

#include 
#include 
#include 

// 每个节点的子节点数量
// 我们将构建一个N叉树并使其成为字典树
// 由于我们有26个英文字母，每个节点需要
// 26个子节点
#define N 26

typedef struct TrieNode TrieNode;

struct TrieNode {
    // 字典树节点结构
    // 每个节点有N个子节点，从根节点开始
    // 以及一个标记是否为叶节点的标志
    char data; // 仅用于打印目的存储
    TrieNode* children[N];
    int is_leaf;
};

TrieNode* make_trienode(char data) {
    // 为字典树节点分配内存
    TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
    for (int i=0; i<N; i++)
        node->children[i] = NULL;
    node->is_leaf = 0;
    node->data = data;
    return node;
}

void free_trienode(TrieNode* node) {
    // 释放字典树节点序列
    for(int i=0; i<N; i++) {
        if (node->children[i] != NULL) {
            free_trienode(node->children[i]);
        }
        else {
            continue;
        }
    }
    free(node);
}

TrieNode* insert_trie(TrieNode* root, char* word) {
    // 将单词插入到字典树中
    // 假设：单词只包含小写字符
    TrieNode* temp = root;

    for (int i=0; word[i] != '\0'; i++) {
        // 获取字母表中的相对位置
        int idx = (int) word[i] - 'a';
        if (temp->children[idx] == NULL) {
            // 如果相应的子节点不存在，
            // 就创建该子节点！
            temp->children[idx] = make_trienode(word[i]);
        }
        else {
            // 什么都不做。节点已经存在
        }
        // 向下一层，到idx引用的子节点
        // 因为我们有前缀匹配
        temp = temp->children[idx];
    }
    // 在单词的末尾，将此节点标记为叶节点
    temp->is_leaf = 1;
    return root;
}

int search_trie(TrieNode* root, char* word)
{
    // 在字典树中搜索单词
    TrieNode* temp = root;

    for(int i=0; word[i]!='\0'; i++)
    {
        int position = word[i] - 'a';
        if (temp->children[position] == NULL)
            return 0;
        temp = temp->children[position];
    }
    if (temp != NULL && temp->is_leaf == 1)
        return 1;
    return 0;
}

void print_trie(TrieNode* root) {
    // 打印字典树的节点
    if (!root)
        return;
    TrieNode* temp = root;
    printf("%c -> ", temp->data);
    for (int i=0; i<N; i++) {
        print_trie(temp->children[i]); 
    }
}

void print_search(TrieNode* root, char* word) {
    printf("搜索 %s: ", word);
    if (search_trie(root, word) == 0)
        printf("未找到\n");
    else
        printf("已找到！\n");
}

int main() {
    // 字典树数据结构操作的驱动程序
    TrieNode* root = make_trienode('\0');
    root = insert_trie(root, "hello");
    root = insert_trie(root, "hi");
    root = insert_trie(root, "teabag");
    root = insert_trie(root, "teacan");
    print_search(root, "tea");
    print_search(root, "teabag");
    print_search(root, "teacan");
    print_search(root, "hi");
    print_search(root, "hey");
    print_search(root, "hello");
    print_trie(root);
    free_trienode(root);
    return 0;
}

使用gcc编译器编译后，你将得到以下输出：

搜索 for tea: 未找到
搜索 for teabag: 已找到！
搜索 for teacan: 已找到！
搜索 for hi: 已找到！
搜索 for hey: 未找到
搜索 for hello: 已找到！
 -> h -> e -> l -> l -> o -> i -> t -> e -> a -> b -> a -> g -> c -> a -> n ->

虽然打印方式可能不太直观，但关键在于查看print_trie()方法。因为该方法首先打印当前节点，然后打印其所有子节点，所以这个顺序确实表明了打印的顺序。

那么，现在让我们来实现删除方法吧！

从字典树数据结构中删除一个单词

这个方法比另外两个方法稍微复杂一些。

由于我们没有明确存储键和值的方式，因此不存在任何格式算法。

然而，针对本文的目的，我只会处理那些待删除的词是叶节点的情况。也就是说，它必须完全匹配前缀，直至达到一个叶节点。

那么让我们开始吧。我们删除函数的签名将是：

TrieNode* delete_trie(TrieNode* root, char* word);

在前面提到过，只有当匹配的前缀达到叶节点时，才会执行删除操作。因此，让我们编写另一个函数is_leaf_node()来为我们执行此操作。

int is_leaf_node(TrieNode* root, char* word) {
    // Checks if the prefix match of word and root
    // is a leaf node
    TrieNode* temp = root;
    for (int i=0; word[i]; i++) {
        int position = (int) word[i] - 'a';
        if (temp->children[position]) {
            temp = temp->children[position];
        }
    }
    return temp->is_leaf;
}

好的，完成了之后，让我们来看一下我们的delete_trie()方法的草稿。

TrieNode* delete_trie(TrieNode* root, char* word) {
    // Will try to delete the word sequence from the Trie only it 
    // ends up in a leaf node
    if (!root)
        return NULL;
    if (!word || word[0] == '\0')
        return root;
    // If the node corresponding to the match is not a leaf node,
    // we stop
    if (!is_leaf_node(root, word)) {
        return root;
    }
    // TODO
}

经过这个检查之后，我们现在知道我们的词将以叶节点结束。

但还有另外一种情况需要处理。如果存在另一个单词与当前字符串具有部分前缀匹配的情况怎么办？

例如，在下面的字典树中，单词”tea”和”ted”在”te”之前有部分相同的匹配。

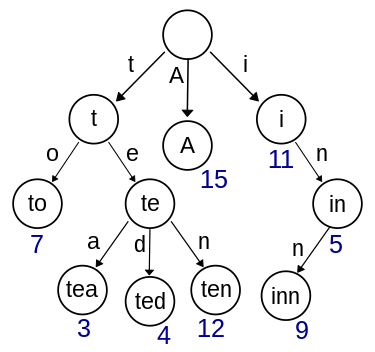
所以，如果发生这种情况，我们不能简单地从t到a删除整个序列，因为它们是链接在一起的，那样两个链都会被删除！

因此，我们需要找到能够出现这种匹配的最深点。只有在那之后，我们才能删除剩余的链条。

这涉及到查找最长的前缀字符串，所以让我们写另一个函数。

char* longest_prefix(TrieNode* root, char* word);

这将返回字典树中的最长匹配，该匹配并非当前的单词。下面的代码在注释中解释了每个中间步骤。

char* find_longest_prefix(TrieNode* root, char* word) {
    // 查找字典树中单词的最长公共前缀子字符串
    if (!word || word[0] == '\0')
        return NULL;
    // 最长前缀的长度
    int len = strlen(word);

    // 我们最初将最长前缀设置为单词本身，
    // 并尝试从最深位置回溯到
    // 分歧点（如果存在）
    char* longest_prefix = (char*) calloc (len + 1, sizeof(char));
    for (int i=0; word[i] != '\0'; i++)
        longest_prefix[i] = word[i];
    longest_prefix[len] = '\0';

    // 如果从根节点没有分支，这意味着
    // 我们正在匹配原始字符串！
    // 这不是我们想要的！
    int branch_idx  = check_divergence(root, longest_prefix) - 1;
    if (branch_idx >= 0) {
        // 存在分支，我们必须更新位置
        // 到最长匹配处，并通过分支索引长度
        // 更新最长前缀
        longest_prefix[branch_idx] = '\0';
        longest_prefix = (char*) realloc (longest_prefix, (branch_idx + 1) * sizeof(char));
    }

    return longest_prefix;
}

这里还有一个变化！由于我们试图找到最长的匹配，算法实际上会贪婪地匹配原始字符串本身！这不是我们想要的。

我们希望找到最长的匹配项，但排除原始输入字符串。因此，我们必须使用另一种方法check_divergence()进行必要的检查。

这将检查从根节点到当前位置是否存在任何分支，并返回最佳匹配的长度，该长度不是输入的长度。

如果我们处于坏链中，对应于原始字符串，那么就不会从该点分叉！所以对于我们来说，使用check_divergence()是避免那个讨厌的点的好方法。

int check_divergence(TrieNode* root, char* word) {
    // 检查单词的最后一个字符处是否存在分支
 // 并返回单词中发生分支的最大位置
    TrieNode* temp = root;
    int len = strlen(word);
    if (len == 0)
        return 0;
    // 我们将返回发生分支的最大索引
    int last_index = 0;
    for (int i=0; i < len; i++) {
        int position = word[i] - 'a';
        if (temp->children[position]) {
            // 如果该位置存在子节点
            // 我们将检查是否存在任何其他子节点
            // 以便发生分支
            for (int j=0; j<N; j++) {
                if (j != position && temp->children[j]) {
                    // 我们找到了另一个子节点！这是一个分支。
                    // 更新分支位置
                    last_index = i + 1;
                    break;
                }
            }
            // 移动到序列中的下一个子节点
            temp = temp->children[position];
        }
    }
    return last_index;
}

最后，我们确保不会盲目地删除整个链条。所以现在让我们继续使用我们的删除方法。

TrieNode* delete_trie(TrieNode* root, char* word) {
    // 仅当单词序列最终以叶子节点结束时
    // 才尝试从字典树中删除该单词序列
    if (!root)
        return NULL;
    if (!word || word[0] == '\0')
        return root;
    // 如果对应于匹配的节点不是叶子节点，
    // 我们停止
    if (!is_leaf_node(root, word)) {
        return root;
    }
    TrieNode* temp = root;
    // 查找不是当前单词的最长前缀字符串
    char* longest_prefix = find_longest_prefix(root, word);
    //printf("Longest Prefix = %s\n", longest_prefix);
    if (longest_prefix[0] == '\0') {
        free(longest_prefix);
        return root;
    }
    // 跟踪在字典树中的位置
    int i;
    for (i=0; longest_prefix[i] != '\0'; i++) {
        int position = (int) longest_prefix[i] - 'a';
        if (temp->children[position] != NULL) {
            // 继续移动到公共前缀中的最深节点
            temp = temp->children[position];
        }
        else {
            // 没有这样的节点。直接返回。
            free(longest_prefix);
            return root;
        }
    }
    // 现在，我们已经到达两个字符串之间的最深公共节点。
    // 我们需要删除对应于单词的序列
    int len = strlen(word);
    for (; i < len; i++) {
        int position = (int) word[i] - 'a';
        if (temp->children[position]) {
            // 删除剩余的序列
            TrieNode* rm_node = temp->children[position];
            temp->children[position] = NULL;
            free_trienode(rm_node);
        }
    }
    free(longest_prefix);
    return root;
}

上述的代码简单地找到了前缀匹配的最深节点，并从字典树中删除剩余匹配的单词序列，因为这与任何其他的匹配无关。

上述过程的时间复杂度

字典树操作的时间复杂度

操作 时间复杂度
search_trie() O(n) – 其中 n 是输入字符串的长度
insert_trie() O(n) – 其中 n 是输入字符串的长度
delete_trie() O(C*n) – 其中 C 是字母表中的字母数量，
n 是输入单词的长度

几乎所有情况下，字母的数量是恒定的，因此 delete_trie() 的复杂度也被降低到 O(n)。

字典树数据结构的完整C/C++程序

最终，我们（希望如此）完成了delete_trie()函数。让我们使用我们的驱动程序来检查我们所编写的是否正确。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 每个节点的子节点数量
// 我们将构建一个N叉树并使其成为Trie
// 由于我们有26个英文字母，每个节点需要
// 26个子节点
#define N 26

typedef struct TrieNode TrieNode;

struct TrieNode {
    // Trie节点结构
    // 每个节点有N个子节点，从根节点开始
    // 以及一个标志来检查它是否是叶节点
    char data; // 仅用于打印目的而存储
    TrieNode* children[N];
    int is_leaf;
};

TrieNode* make_trienode(char data) {
    // 为TrieNode分配内存
    TrieNode* node = (TrieNode*) calloc (1, sizeof(TrieNode));
    for (int i=0; i<N; i++)
        node->children[i] = NULL;
    node->is_leaf = 0;
    node->data = data;
    return node;
}

void free_trienode(TrieNode* node) {
    // 释放trienode序列
    for(int i=0; i<N; i++) {
        if (node->children[i] != NULL) {
            free_trienode(node->children[i]);
        }
        else {
            continue;
        }
    }
    free(node);
}

TrieNode* insert_trie(TrieNode* root, char* word) {
    // 将单词插入到Trie中
    // 假设：单词只包含小写字符
    TrieNode* temp = root;

    for (int i=0; word[i] != '\0'; i++) {
        // 获取字母表中的相对位置
        int idx = (int) word[i] - 'a';
        if (temp->children[idx] == NULL) {
            // 如果相应的子节点不存在，
            // 只需创建该子节点！
            temp->children[idx] = make_trienode(word[i]);
        }
        else {
            // 什么都不做。节点已经存在
        }
        // 向下一级，到idx引用的子节点
        // 因为我们有前缀匹配
        temp = temp->children[idx];
    }
    // 在单词的末尾，将此节点标记为叶节点
    temp->is_leaf = 1;
    return root;
}

int search_trie(TrieNode* root, char* word)
{
    // 在Trie中搜索单词
    TrieNode* temp = root;

    for(int i=0; word[i]!='\0'; i++)
    {
        int position = word[i] - 'a';
        if (temp->children[position] == NULL)
            return 0;
        temp = temp->children[position];
    }
    if (temp != NULL && temp->is_leaf == 1)
        return 1;
    return 0;
}

int check_divergence(TrieNode* root, char* word) {
    // 检查单词的最后一个字符是否有分支
    // 并返回单词中出现分支的最大位置
    TrieNode* temp = root;
    int len = strlen(word);
    if (len == 0)
        return 0;
    // 我们将返回出现分支的最大索引
    int last_index = 0;
    for (int i=0; i < len; i++) {
        int position = word[i] - 'a';
        if (temp->children[position]) {
            // 如果该位置存在子节点
            // 我们将检查是否存在任何其他子节点
            // 以便发生分支
            for (int j=0; j<N; j++) {
                if (j != position && temp->children[j]) {
                    // 我们找到了另一个子节点！这是一个分支。
                    // 更新分支位置
                    last_index = i + 1;
                    break;
                }
            }
            // 转到序列中的下一个子节点
            temp = temp->children[position];
        }
    }
    return last_index;
}

char* find_longest_prefix(TrieNode* root, char* word) {
    // 在Trie中查找单词的最长公共前缀子串
    if (!word || word[0] == '\0')
        return NULL;
    // 最长前缀的长度
    int len = strlen(word);

    // 我们最初将最长前缀设置为单词本身，
    // 并尝试从最深位置回溯
    // 到一个分歧点，如果存在的话
    char* longest_prefix = (char*) calloc (len + 1, sizeof(char));
    for (int i=0; word[i] != '\0'; i++)
        longest_prefix[i] = word[i];
    longest_prefix[len] = '\0';

    // 如果从根节点没有分支，这意味着
    // 我们正在匹配原始字符串！
    // 这不是我们想要的！
    int branch_idx  = check_divergence(root, longest_prefix) - 1;
    if (branch_idx >= 0) {
        // 存在分支，我们必须更新位置
        // 到最长匹配并更新最长前缀
        // 通过分支索引长度
        longest_prefix[branch_idx] = '\0';
        longest_prefix = (char*) realloc (longest_prefix, (branch_idx + 1) * sizeof(char));
    }

    return longest_prefix;
}

int is_leaf_node(TrieNode* root, char* word) {
    // 检查单词和根节点的前缀匹配
    // 是否是叶节点
    TrieNode* temp = root;
    for (int i=0; word[i]; i++) {
        int position = (int) word[i] - 'a';
        if (temp->children[position]) {
            temp = temp->children[position];
        }
    }
    return temp->is_leaf;
}

TrieNode* delete_trie(TrieNode* root, char* word) {
    // 只有当单词序列以叶节点结束时，
    // 才会尝试从Trie中删除它
    if (!root)
        return NULL;
    if (!word || word[0] == '\0')
        return root;
    // 如果对应于匹配的节点不是叶节点，
    // 我们停止
    if (!is_leaf_node(root, word)) {
        return root;
    }
    TrieNode* temp = root;
    // 查找不是当前单词的最长前缀字符串
    char* longest_prefix = find_longest_prefix(root, word);
    //printf("Longest Prefix = %s\n", longest_prefix);
    if (longest_prefix[0] == '\0') {
        free(longest_prefix);
        return root;
    }
    // 跟踪在Trie中的位置
    int i;
    for (i=0; longest_prefix[i] != '\0'; i++) {
        int position = (int) longest_prefix[i] - 'a';
        if (temp->children[position] != NULL) {
            // 继续移动到公共前缀中的最深节点
            temp = temp->children[position];
        }
        else {
            // 没有这样的节点。只需返回。
            free(longest_prefix);
            return root;
        }
    }
    // 现在，我们已经到达两个字符串之间最深的公共节点。
    // 我们需要删除对应于单词的序列
    int len = strlen(word);
    for (; i < len; i++) {
        int position = (int) word[i] - 'a';
        if (temp->children[position]) {
            // 删除剩余的序列
            TrieNode* rm_node = temp->children[position];
            temp->children[position] = NULL;
            free_trienode(rm_node);
        }
    }
    free(longest_prefix);
    return root;
}

void print_trie(TrieNode* root) {
    // 打印trie的节点
    if (!root)
        return;
    TrieNode* temp = root;
    printf("%c -> ", temp->data);
    for (int i=0; i<N; i++) {
        print_trie(temp->children[i]); 
    }
}

void print_search(TrieNode* root, char* word) {
    printf("查找 %s: ", word);
    if (search_trie(root, word) == 0)
        printf("未找到\n");
    else
        printf("已找到！\n");
}

int main() {
    // Trie数据结构操作的驱动程序
    TrieNode* root = make_trienode('\0');
    root = insert_trie(root, "hello");
    root = insert_trie(root, "hi");
    root = insert_trie(root, "teabag");
    root = insert_trie(root, "teacan");
    print_search(root, "tea");
    print_search(root, "teabag");
    print_search(root, "teacan");
    print_search(root, "hi");
    print_search(root, "hey");
    print_search(root, "hello");
    print_trie(root);
    printf("\n");
    root = delete_trie(root, "hello");
    printf("删除 'hello' 后...\n");
    print_trie(root);
    printf("\n");
    root = delete_trie(root, "teacan");
    printf("删除 'teacan' 后...\n");
    print_trie(root);
    printf("\n");
    free_trienode(root);
    return 0;
}

程序输出

查找 tea: 未找到
查找 teabag: 已找到！
查找 teacan: 已找到！
查找 hi: 已找到！
查找 hey: 未找到
查找 hello: 已找到！
 -> h -> e -> l -> l -> o -> i -> t -> e -> a -> b -> a -> g -> c -> a -> n -> 
删除 'hello' 后...
 -> h -> i -> t -> e -> a -> b -> a -> g -> c -> a -> n -> 
删除 'teacan' 后...
 -> h -> i -> t -> e -> a -> b -> a -> g ->

通过这个例子，我们已经完成了在C/C++中实现Trie数据结构的学习。我知道这是一篇很长的阅读，但希望你能正确理解如何应用这些方法！

下载该代码

这是文章《C/C++中的字典树数据结构》的第7部分（共7部分）。

内容片段: 你可以在我上传到Github代码片段上找到完整的代码。它可能不是最高效的代码，但我已尽力确保它能正常工作。

如果你有任何问题或建议，欢迎在下方的评论区提出！

参考资料

  • 维基百科关于字典树的文章

推荐阅读

如果你对类似的话题感兴趣，可以参考《数据结构和算法》部分，其中包括哈希表和图论等主题。

bannerAds