Java/C++回溯法实战:N皇后问题的高效解决方案与代码实现
如果你喜欢下棋,你会喜欢学习N皇后问题。这是一个很好的问题,可以帮助你理解回溯算法。
什么是回溯法?
在回溯法中,我们从众多可行的移动中选择一个开始。然后我们尝试解决问题。
如果我们能够通过选择的移动来解决问题,那么我们将打印解决方案。否则,我们将回溯并选择其他移动,尝试解决问题。
如果所有的解决方案都不起作用,我们宣称这个问题没有解决方案。
N皇后问题是什么?
如何在NxN的棋盘上放置N个皇后,使得它们之间不会互相攻击?
这个问题在N=4和N=8时经常出现。
让我们来看一个N=4的例子。
在解决问题之前,你需要了解国际象棋中皇后的移动方式。
一位皇后可以向任意方向移动任意数量的步骤。唯一的限制是,它在移动过程中不能改变方向。
通过观察皇后的移动可以清楚地看出一件事,即没有两个皇后可以位于同一行或同一列。
这使得我们只能在每一行和每一列上放置一个皇后。
当N等于4时,解决方案如下:
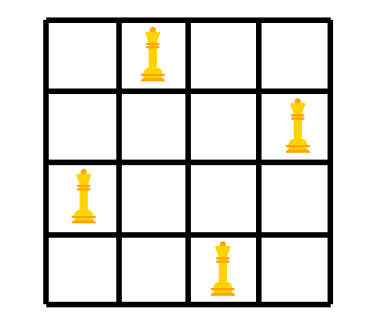
但是我们如何取得这个安排?
N-皇后问题的解决方案
我们解决这个问题的方式是在一个位置上放置一枚皇后,并试图排除其被攻击的可能性。我们在每一行/每一列都放置一个皇后。
如果我们发现皇后在已选的位置受到攻击,我们尝试下一个位置。
如果一个皇后在一排的所有位置上都受到攻击,我们将回溯并改变先前位置放置的皇后的位置。
我们不断重复放置皇后并进行回溯的过程,直到所有N个皇后都成功地放置完成。
以下是逐步回溯的步骤展示:
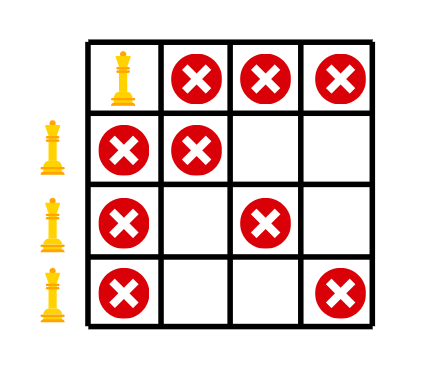
红色十字标志着在攻击中的位置,这些位置受到皇后的威胁。每当我们遇到一种情况,所有行中的位置都受到攻击,但我们又有一个要放置的皇后时,我们就会回溯。
这并不是问题的唯一解决方案。如果你按照顺时针的方式将每个皇后向前移动一步,就会得到另一个解决方案。
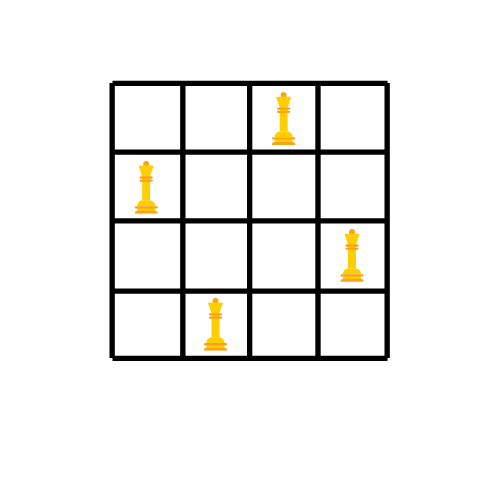
在这个例子中,我们按照行来摆放皇后,我们也可以按照列进行相同的操作。那样的话,每个皇后将属于一列。
使用C++和Java实现N皇后问题
在C++中实现N皇后问题。
#define N 4
#include <stdbool.h>
#include <stdio.h>
// 打印解决方案的函数
void printSolution(int board[N][N])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
printf(" %d ", board[i][j]);
printf("\n");
}
}
// 检查位置是否安全的函数
bool isSafe(int board[N][N], int row, int col)
{
int i, j;
for (i = 0; i < col; i++)
if (board[row][i])
return false;
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j])
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j])
return false;
return true;
}
// 使用回溯法解决问题的函数
bool solveNQUtil(int board[N][N], int col)
{
if (col >= N)
return true;
for (int i = 0; i < N; i++) {
// 如果在位置 i,col 放置皇后是安全的,则放置它
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQUtil(board, col + 1))
return true;
// 如果上述条件为假,则回溯
board[i][col] = 0; // 回溯
}
}
return false;
}
// 测试上述函数的主程序
int main()
{
int board[N][N] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (solveNQUtil(board, 0) == false) {
printf("解决方案不存在");
return 0;
}
printSolution(board);
return true;
return 0;
}
在C++中实现N皇后问题。
package com.JournalDev;
public class Main {
static final int N = 4;
// 打印最终解决方案矩阵
static void printSolution(int board[][])
{
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++)
System.out.print(" " + board[i][j]
+ " ");
System.out.println();
}
}
// 检查位置是否安全的函数
static boolean isSafe(int board[][], int row, int col)
{
int i, j;
for (i = 0; i < col; i++)
if (board[row][i] == 1)
return false;
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j] == 1)
return false;
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j] == 1)
return false;
return true;
}
// 使用回溯法解决问题的函数
public static boolean solveNQueen(int board[][], int col)
{
if (col >= N)
return true;
for (int i = 0; i < N; i++) {
//如果在位置i,col放置皇后是安全的 -> 放置它
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQueen(board, col + 1))
return true;
//如果上述条件为假,则回溯
board[i][col] = 0;
}
}
return false;
}
public static void main(String args[])
{
int board[][] = { { 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 },
{ 0, 0, 0, 0 } };
if (!solveNQueen(board, 0)) {
System.out.print("解决方案不存在");
return;
}
printSolution(board);
}
}
输出结果:
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0

当N=8时,输出结果为:
1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0
0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1
0 1 0 0 0 0 0 0
0 0 0 1 0 0 0 0
0 0 0 0 0 1 0 0
0 0 1 0 0 0 0 0
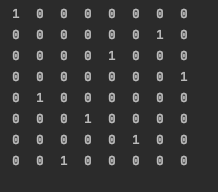
理解代码的实现
为了检查一个位置是否受到攻击,我们创建了一个名为isSafe的函数。
如果位置安全且没有受到攻击,则该函数返回true。
static boolean isSafe(int board[][], int row, int col)
{
int i, j;
// 检查同一行是否有皇后
for (i = 0; i < col; i++)
if (board[row][i] == 1)
return false;
// 检查左上对角线是否有皇后
for (i = row, j = col; i >= 0 && j >= 0; i--, j--)
if (board[i][j] == 1)
return false;
// 检查左下对角线是否有皇后
for (i = row, j = col; j >= 0 && i < N; i++, j--)
if (board[i][j] == 1)
return false;
return true;
}
第一个循环通过列进行检查,第二个和第三个循环通过两个对角线进行检查。
以下代码负责将皇后放置在它们的位置并进行回溯。为了标记皇后的位置,我们将该单元格在矩阵中设置为1。在放置皇后之前,我们调用isSafe函数来确保位置安全。
public static boolean solveNQueen(int board[][], int col)
{
if (col >= N)
return true;
for (int i = 0; i < N; i++) {
//如果在位置(i, col)放置皇后是安全的,则放置它
if (isSafe(board, i, col)) {
board[i][col] = 1;
if (solveNQueen(board, col + 1))
return true;
//如果上述条件为假,则进行回溯
board[i][col] = 0;
}
}
return false;
}
递归调用将棋盘传入并将列设置为col+1。如果递归调用返回false,则通过将该位置重新设置为0来进行回溯。
结论
这是使用回溯法解决N皇后问题的方法。要了解更多关于回溯法的知识,可以尝试解决数独问题。

