用Java实现最大堆数据结构
一个最大堆是一个完全二叉树,其中一个节点的值大于或等于其子节点的值。最大堆数据结构在使用堆排序对数据进行排序时非常有用。
在这个教程中,我们将涵盖你从零开始在Java中实现最大堆所需要的所有知识。
在Java中实现一个最大堆数据结构
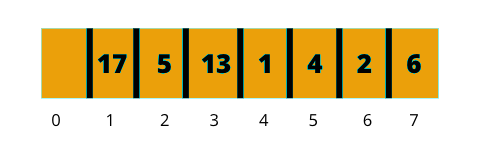
我们使用数组来表示堆。由于堆是完全二叉树,所以不会浪费空间。
例如,让我们以以下方式考虑一个堆:
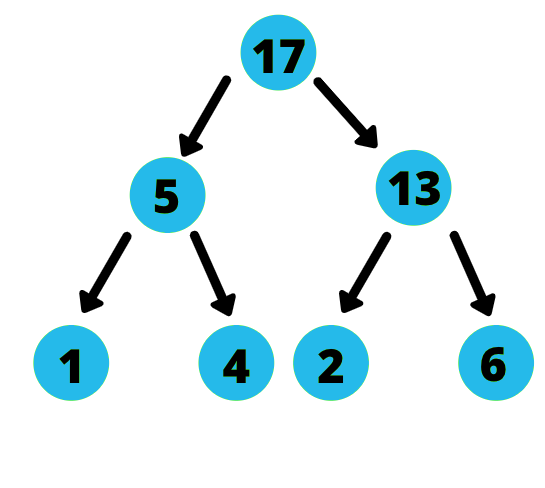
数组表示为:
最大堆的声明方式如下:
static class MaxHeap {
private int[] Heap; // array
private int size;
private int maxsize;
public MaxHeap(int size) {
this.maxsize = size;
this.size = 0;
Heap = new int[this.maxsize + 1];
Heap[0] = Integer.MAX_VALUE;
}
堆是存储最大堆的数组。构造函数接受大小并将数组的第0个元素初始化为无穷大。我们从索引1开始构建我们的堆。
获取节点的父节点 (Huòqǔ jiédiǎn de fù jiédian)
由于我们将堆存储为一个数组,因此获取节点的父节点变得更容易了。
对于位置 i 上的元素,其父元素的位置由下式给出:
(i)/2
在执行过程中,我们可以通过使用以下方法获取父级对象:
private int parent(int pos) {
return pos / 2;
}
2. 为节点获取子节点
对于位于位置i的节点,它的子节点由以下公式给出:
左侧的孩子:
(2*i)
右孩子
(2*i)+ 1
注意:这只适用于当你的堆从索引1开始的情况。如果堆从位置0开始,则左孩子和右孩子的值分别为(2*i) +1和(2*i) +2。
在代码中,我们按照以下方式进行实现。
private int leftChild(int pos) {
return (2 * pos) ;
}
private int rightChild(int pos) {
return (2 * pos) + 1;
}
3. 对新插入的元素进行堆化处理
将一个元素插入堆后,它可能不满足堆的性质。这种情况下,我们需要调整堆的位置使其重新成为堆。这个过程被称为堆化。
将一个元素进行堆化时,我们需要找到其子节点中的最大值,并将其与当前元素进行交换。我们重复这个过程,直到每个节点都满足堆的性质。
为了实现堆化,我们从根节点向叶子节点移动。因此,这也被称为下沉堆化。
另一个值得注意的有趣点是我们只对非叶节点执行下推(down heapify)。
下移函数的代码是:
private void downHeapify(int pos) {
//checking if the node is a leaf node
if (pos >= (size / 2) && pos <= size)
return;
//checking if a swap is needed
if (Heap[pos] < Heap[leftChild(pos)] ||
Heap[pos] < Heap[rightChild(pos)]) {
//replacing parent with maximum of left and right child
if (Heap[leftChild(pos)] > Heap[rightChild(pos)]) {
swap(pos, leftChild(pos));
//after swaping, heapify is called on the children
downHeapify(leftChild(pos));
} else {
swap(pos, rightChild(pos));
//after swaping, heapify is called on the children
downHeapify(rightChild(pos));
}
}
}
交换函数如下:
private void swap(int fpos, int spos) {
int tmp;
tmp = Heap[fpos];
Heap[fpos] = Heap[spos];
Heap[spos] = tmp;
}
您还可以使用 while 循环而不是递归来编写相同的代码。
在下溢(down-heapify)的过程中,我们是从父节点向子节点移动的。我们也可以采用自底向上的方式进行移动。当我们以自底向上的方式移动时,我们将一个节点与它的父节点进行比较。这被称为上溢(Up Heapify)。
向上堆化的代码是:
private void heapifyUp(int pos) {
int temp = Heap[pos];
while(pos>0 && temp > Heap[parent(pos)]){
Heap[pos] = Heap[parent(pos)];
pos = parent(pos);
}
Heap[pos] = temp;
}
我们使用while循环而不是递归编写了up heapify的代码。
4. 插入新的节点
数组的末尾添加了一个新元素,并进行互换以确保堆属性的成立。
插入的算法是:
- 增加堆大小
将新元素保留在堆(数组)的末尾
从底部向顶部进行堆化
插入的代码是:
public void insert(int element) {
Heap[++size] = element;
int current = size;
heapifyUp(current);
}
5. 删除/提取节点
从堆中删除/提取一个节点,我们从根节点删除该元素。根节点总是提供最大的元素。
删除的算法如下:
- 将第一个元素复制到一个变量中。
将最后一个元素复制到第一个位置(根)。
调用 downHeapify()。
删除的代码是:
public int extractMax() {
int max = Heap[1];
Heap[1] = Heap[size--];
downHeapify(1);
return max;
}
在这里我们使用 size– 来减少堆的大小。
Java中完整实现Max Heap
完整的Java最大堆的实现如下。
package com.JournalDev;
public class Main {
static class MaxHeap {
private int[] Heap;
private int size;
private int maxsize;
public MaxHeap(int size) {
this.maxsize = size;
this.size = 0;
Heap = new int[this.maxsize + 1];
Heap[0] = Integer.MAX_VALUE;
}
private int parent(int pos) {
return pos / 2;
}
private int leftChild(int pos) {
return (2 * pos) ;
}
private int rightChild(int pos) {
return (2 * pos) + 1;
}
private void swap(int fpos, int spos) {
int tmp;
tmp = Heap[fpos];
Heap[fpos] = Heap[spos];
Heap[spos] = tmp;
}
private void downHeapify(int pos) {
if (pos >= (size / 2) && pos <= size)
return;
if (Heap[pos] < Heap[leftChild(pos)] ||
Heap[pos] < Heap[rightChild(pos)]) {
if (Heap[leftChild(pos)] > Heap[rightChild(pos)]) {
swap(pos, leftChild(pos));
downHeapify(leftChild(pos));
} else {
swap(pos, rightChild(pos));
downHeapify(rightChild(pos));
}
}
}
private void heapifyUp(int pos) {
int temp = Heap[pos];
while(pos>0 && temp > Heap[parent(pos)]){
Heap[pos] = Heap[parent(pos)];
pos = parent(pos);
}
Heap[pos] = temp;
}
public void insert(int element) {
Heap[++size] = element;
int current = size;
heapifyUp(current);
}
public void print() {
for (int i = 1; i <= size / 2; i++) {
System.out.print(+ Heap[i] + ": L- " +
Heap[2 * i] + " R- " + Heap[2 * i + 1]);
System.out.println();
}
}
public int extractMax() {
int max = Heap[1];
Heap[1] = Heap[size--];
downHeapify(1);
return max;
}
}
public static void main(String[] arg)
{
MaxHeap maxHeap = new MaxHeap(15);
maxHeap.insert(1);
maxHeap.insert(4);
maxHeap.insert(2);
maxHeap.insert(5);
maxHeap.insert(13);
maxHeap.insert(6);
maxHeap.insert(17);
maxHeap.print();
System.out.println("The max is " + maxHeap.extractMax());
}
}
Output :
17: L- 5 R- 13
5: L- 1 R- 4
13: L- 2 R- 6
The max is 17
结论
这个教程是关于Java中最大堆数据结构的。

