在二叉树中进行层次遍历

层次遍历是一种横向遍历二叉树的方法之一。在本文中，我们将讨论如何在C/C++中实现这个算法。

但在此之前，让我们先梳理一下我们的概念。

---

构建概念

二叉树是一种数据结构，每个节点最多有两个子节点。最上方的节点被称为根节点。

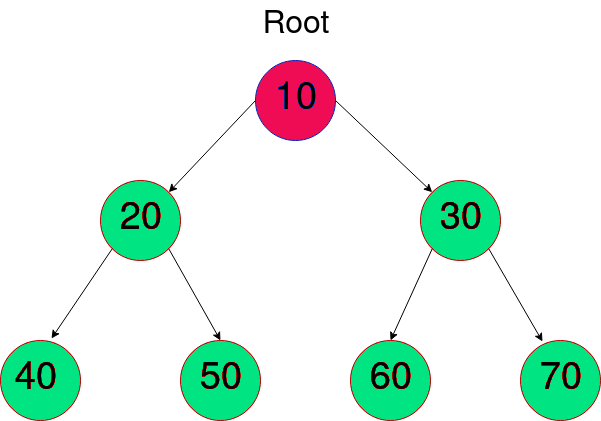
遍历二叉树的常见方式有四种，分别是：

• In order Traversal
• Pre Order Traversal
• Post Order Traversal
• Level Order Traversal

让我们来了解二叉树中的层级意味着什么。

一个级别是树中与给定节点对应的父节点的数量。基本上就是从该节点到根节点的祖先数量。

所以，对于根节点（最顶层节点）而言，它的层级是0，因为它没有父节点。如果它有子节点，那么它们的层级都会是1，因为在根节点之前它们只有一个祖先，即根节点本身。

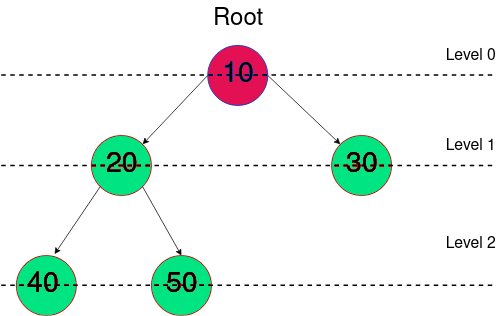
我们还需要理解二叉树中的高度概念。这其实就是从根节点到树中最深节点的路径长度。

在这种情况下，高度将是从最深叶节点（40或50，因为它们具有最大层级）到根的长度。因此，树的高度为2。

现在我们已经掌握了概念，让我们来了解如何实施层序遍历。

---

层次遍历

层次遍历是一种总是根据树的层级进行遍历的方法。

所以，这个遍历首先遍历与Level 0相对应的节点，然后是Level 1，依此类推，从根节点开始。

在上面的二叉树例子中，层序遍历的顺序将会是：

（起始值）10 – > 20 -> 30 -> 40 -> 50

为了做到这一点，我们需要做两件事情。

我们首先必须找出这棵树的高度。
我们需要找到一种方法来打印每个层级对应的节点。

找到树的高度

首先我们会找到树的高度。要做到这一点，逻辑很简单。

由于树的高度被定义为从根节点到叶子节点的最长路径，因此我们可以递归地计算左右子树的高度，并找到子树中的最大高度。树的高度将简单地等于子树的高度加1。

C-风格的伪代码：

// Find height of a tree, defined by the root node
int tree_height(Node* root) {
    if (root == NULL) 
        return 0;
    else {
        // Find the height of left, right subtrees
        left_height = tree_height(root->left);
        right_height = tree_height(root->right);
        
        // Find max(subtree_height) + 1 to get the height of the tree
        return max(left_height, right_height) + 1;
}

打印每一级的所有节点。

现在我们已经有了树的高度，我们需要为每个层级打印节点。为了做到这一点，我们将使用一个for循环来迭代所有层级直到树的高度，并打印每个层级的节点。

void print_tree_level_order(Node* root) {
    int height = tree_height(root);
    for (int i=0; i<height; i++) {
        // Print the ith level
        print_level(root, i);
    }
}

观察到我们需要另一个函数来打印树的第i层。

再次，我们有一个类似的逻辑。但这次，在打印根节点后，我们将根节点更改为其左子节点和右子节点，并打印两个子树。

直到我们到达叶子节点，也就是辅助根节点在下一步将为NULL的时候，这将会继续进行。（因为叶子节点的左指向NULL且右指向NULL）

void print_level(Node* root, int level_no) {
    // Prints the nodes in the tree
    // having a level = level_no
    
    // We have a auxiliary root node
    // for printing the root of every
    // sub-tree
    if (!root)
        return;
    if (level_no == 0) {
        // We are at the top of a sub-tree
        // So print the auxiliary root node
        printf("%d -> ", root->value);
    }
    else {
        // Make the auxiliary root node to
        // be the left and right nodes for
        // the sub-trees and decrease level by 1, since
        // you are moving from top to bottom
        print_level(root->left, level_no - 1);
        print_level(root->right, level_no - 1);
    }

}

现在，我们终于完成了层序遍历！

我将在下面提供完整的程序，其中还包含使用插入方法构建二叉树的部分。

---

完整的 C/C++ 代码

尽管这原本是一段C程序，但同样可以在C++上编译。

/**
    Code for https://journaldev.com
    File Name: level_order.c
    Purpose: Find the Level Order Traversal of a Binary Tree

    @author Vijay Ramachandran
    @date 28/01/2020
*/

#include <stdio.h>
#include <stdlib.h>

typedef struct Node Node;

// Define the Tree Node here
struct Node {
    int value;
    // Pointers to the left and right children
    Node* left, *right;
};


Node* init_tree(int data) {
    // Creates the tree and returns the
    // root node
    Node* root = (Node*) malloc (sizeof(Node));
    root->left = root->right = NULL;
    root->value = data;
    return root;
}

Node* create_node(int data) {
    // Creates a new node
    Node* node = (Node*) malloc (sizeof(Node));
    node->value = data;
    node->left = node->right = NULL;
    return node;
}

void free_tree(Node* root) {
    // Deallocates memory corresponding
    // to every node in the tree.
    Node* temp = root;
    if (!temp)
        return;
    free_tree(temp->left);
    free_tree(temp->right);
    if (!temp->left && !temp->right) {
        free(temp);
        return;
    }
}

int tree_height(Node* root) {
    // Get the height of the tree
    if (!root)
        return 0;
    else {
        // Find the height of both subtrees
        // and use the larger one
        int left_height = tree_height(root->left);
        int right_height = tree_height(root->right);
        if (left_height >= right_height)
            return left_height + 1;
        else
            return right_height + 1;
    }
}

void print_level(Node* root, int level_no) {
    // Prints the nodes in the tree
    // having a level = level_no
    
    // We have a auxiliary root node
    // for printing the root of every
    // subtree
    if (!root)
        return;
    if (level_no == 0) {
        // We are at the top of a subtree
        // So print the auxiliary root node
        printf("%d -> ", root->value);
    }
    else {
        // Make the auxiliary root node to
        // be the left and right nodes for
        // the subtrees and decrease level by 1, since
        // you are moving from top to bottom
        print_level(root->left, level_no - 1);
        print_level(root->right, level_no - 1);
    }

}

void print_tree_level_order(Node* root) {
    if (!root)
        return;
    int height = tree_height(root);
    for (int i=0; i<height; i++) {
        printf("Level %d: ", i);
        print_level(root, i);
        printf("\n");
    }
    printf("\n\n-----Complete Level Order Traversal:-----\n");
    for (int i=0; i<height; i++) {
        print_level(root, i);
    }
    printf("\n");
}

int main() {
    // Program to demonstrate Level Order Traversal

    // Create the root node having a value of 10
    Node* root = init_tree(10);
    
    // Insert nodes onto the tree
    root->left = create_node(20);
    root->right = create_node(30);
    root->left->left = create_node(40);
    root->left->right = create_node(50);
    
    // Level Order Traversal
    print_tree_level_order(root);

    // Free the tree!
    free_tree(root);
    return 0;
}

输出

Level 0: 10 -> 
Level 1: 20 -> 30 -> 
Level 2: 40 -> 50 -> 


-----Complete Level Order Traversal:-----
10 -> 20 -> 30 -> 40 -> 50 -> 

您还可以通过我为此目的创建的Github gist下载它。（还包含插入代码的部分）

---

结论

希望你对如何在C/C++中实现层序遍历有了更好的理解。如果你有任何问题，请在下面的评论区随时提问！

---