C++を使用した分数ナップサック

この記事では、C++を使用して分数のナップサック問題を解決する方法について学びます。まず、問題の記述を見てから解決策に移ります。この問題は、多くの人気のある古典的な問題の一つです。これは0-1ナップサック問題や0-Nナップサック問題とはかなり異なります。これは貪欲法のアルゴリズムであり、他の2つは動的計画法のアルゴリズムです。

「フラクショナルナップサック」とは何ですか？」

一部の品物の重さと価格のリスト、そして容量Wのバッグ/ナップサックが与えられます。あなたの仕事は、このバッグに入れるすべてのアイテムの価格の合計が、すべての構成において最大になるようにこのバッグを満たすことです。そして、オブジェクトをまるごと収集するか、一部を収集することができます。

分数ナップサック問題のアルゴリズム

よし、この問題を解決するためのアルゴリズムを見てみましょう。この問題に対しては貪欲な解法を実装することになるので、以下は貪欲アルゴリズムの簡単な説明です。

貪欲アルゴリズムとは何ですか？

これらのアルゴリズムでは、各ステップで局所的な最大値/最小値を達成することで、最終的に全体の最大値/最小値を達成することを目指しています。つまり、私たちは各サブ問題の答えを最大化/最小化し、それが全体の問題の最大/最小の答えへと導かれます。

注意：あなたが選ぶ欲張りな選択肢は、安全な選択である必要があります。

安全な手: 初手と同等に信頼できる最適な回答が存在する場合、その手は安全な手と呼ばれます。

貪欲アルゴリズムとの協力戦略

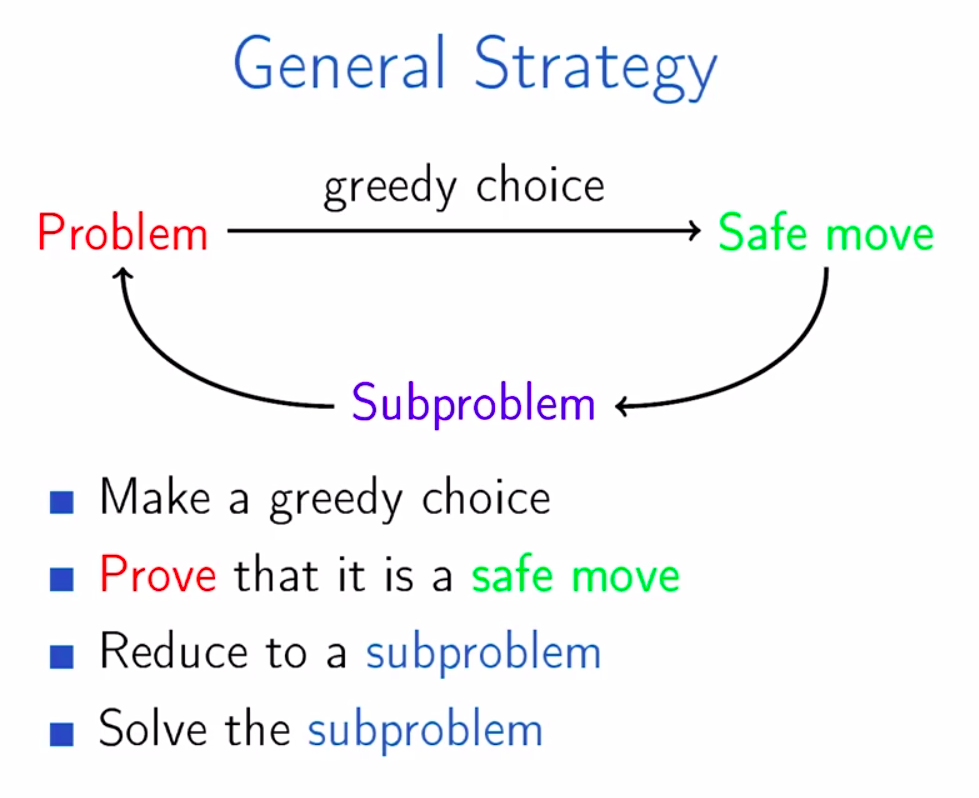
以下は、完璧な貪欲アルゴリズムを開発するためにあなたが従うべき手順です。

• Make a greedy choice
• Prove that it is a safe move so that you don’t write the code and find out in the end that it was not a feasible choice. This particular step is the most important step of greedy algorithms.
• Reduce to a smaller problem
• Solve all the smaller problems.

疑似コード

これから私たちはステップバイステップでナップサックアルゴリズムを進めていきます。

• Sort the items in decreasing order of value/weight ratio. This step alone decreases the time complexity of selection of the best item from O(N) to O(log2N).
• Now we start selecting the objects by running a for loop from i = 0 to i = N
• Lemma: There exists an optimal solution that uses as much as possible of an item with the maximum value per unit of weight.Proof: Try filling the knapsack by a different selection criteria, you will always get smaller total value than the maximum possible value.

以下に添付された例は、私たちの仮説が正しいことを証明しています。 (Sono shita ni tenpuzaremashita rei wa, watashitachi no kahyō ga tadashii koto o shomei shiteimasu.)

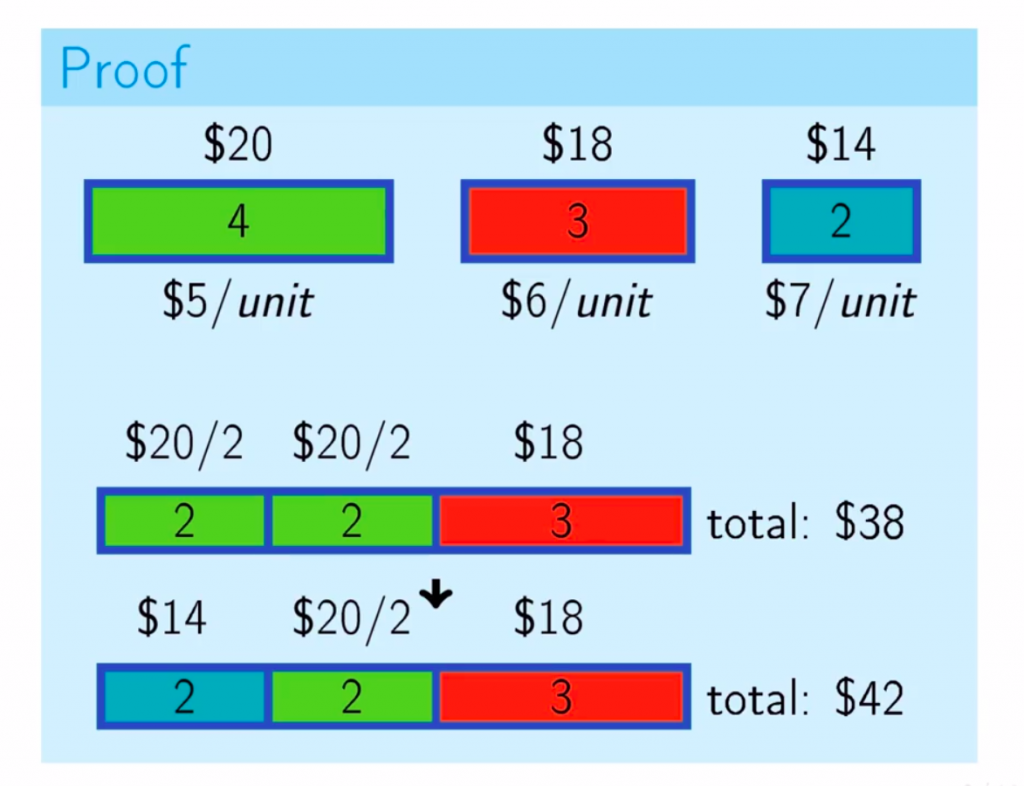
• Now if the size of the item with maximum value/weight ratio fits the knapsack, take the whole of it. Otherwise, take the maximum possible fraction of it.
• Reduce the capacity of the bag by the weight of the item taken.If the whole item is taken then: capacity = capacity – weight[this_item].
  Otherwise, the capacity becomes 0 because the knapsack becomes full.
• Add the value of the fraction of this item taken to the total value.If the whole item is taken: total_value += value[this_item]
  Otherwise, the value += fraction_of_weight_taken * value[this_item].
• If capacity becomes 0, break out of the loop.

疑似コードの全体的な構造は次のようになります:

分数ナップサックを示すC++プログラムを作成します。

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;

// this custom comparator function will allow
// us to compare our vector based on the
// ratio of values to weights
bool compare(pair <float, int> p1, pair <float, int> p2)
{
	return p1.first > p2.first;
}

int fractional_knapsack(vector <int> weights, vector <int> values, int capacity)
{
	int len = weights.size();
	int total_value = 0;

	// vector to store the items based on their value/weight ratios
	vector <pair <float, int>> ratio(len, make_pair(0.0, 0));

	for(int i = 0; i < len; i++)
		ratio[i] = make_pair(values[i]/weights[i], i);

	// now sort the ratios in non-increasing order
	// for this purpose, we will use our custom
	// comparator function
	sort(ratio.begin(), ratio.end(), compare);

	// start selecting the items
	for(int i = 0; i < len; i++)
	{
		if(capacity == 0)
			break;

		int index = ratio[i].second;

		if(weights[index] <= capacity)
		{
			// we item can fit into the knapsack
			// hence take the whole of it
			capacity -= weights[index];

			// add the value of this item to the
			// final answer
			total_value += values[index];
		}
		else
		{
			// this item doesn't fit into the bag
			// and thus we take a fraction of it
			int value_to_consider = values[index] * (float(capacity)/float(weights[index]));
			total_value += value_to_consider;
			capacity = 0;
		}
	}

	return total_value;
}

int main()
{
	cout << "Enter the weights of the items, press -1 to stop" << endl;

	vector <int> weights;

	while(true)
	{
		int weight;
		cin >> weight;

		if(weight == -1)
			break;

		weights.push_back(weight);
	}

	cout << "Enter the values of each item, press -1 to stop" << endl;
	
	vector <int> values;

	while(true)
	{
		int value;
		cin >> value;

		if(value == -1)
			break;

		values.push_back(value);
	}

	cout << "Enter the capacity of the knapsack" << endl;

	int capacity;
	cin >> capacity;

	cout << "The maximum value possible based on current list is: " << fractional_knapsack(weights, values, capacity) << endl;
}

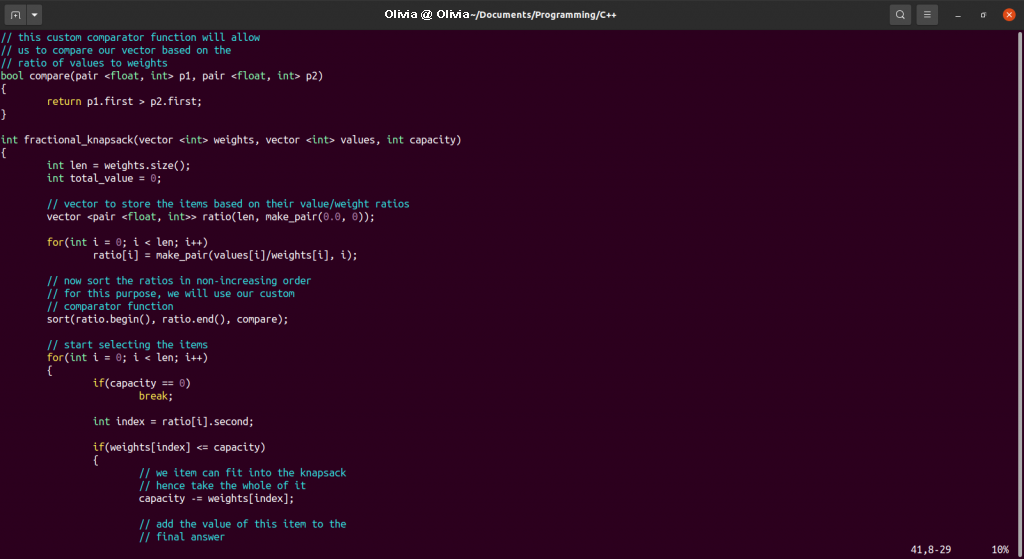
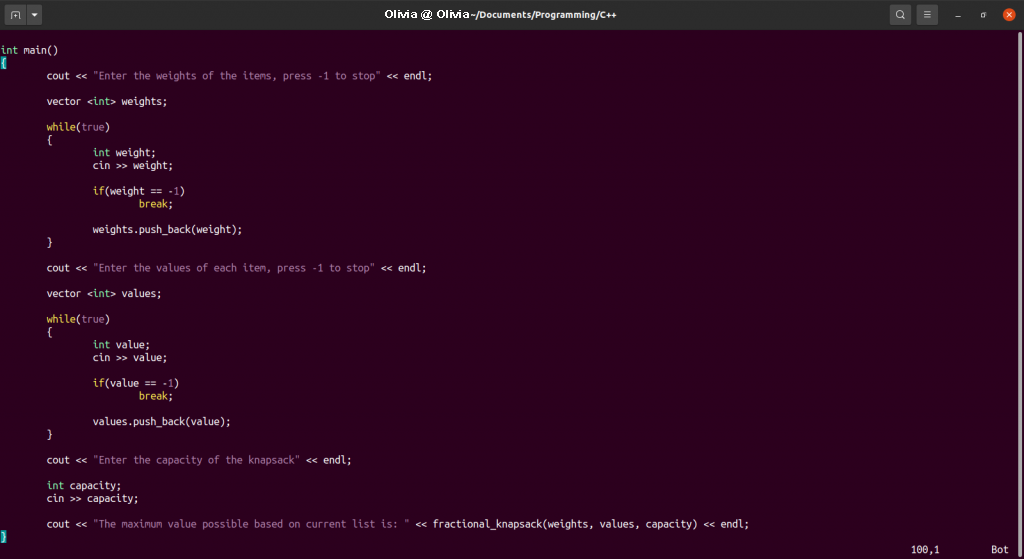
出力

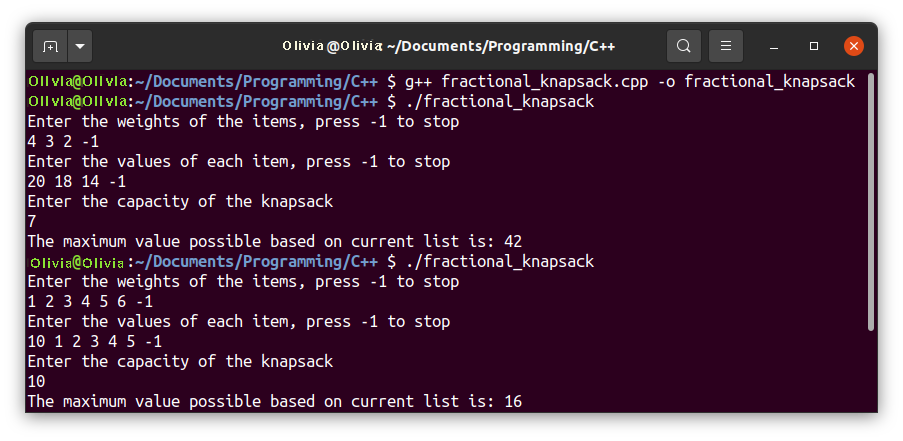
結論

分数ナップサック問題は貪欲アルゴリズムであり、この記事ではその実装を見ました。貪欲アルゴリズムについて簡単に学び、そして分数ナップサックアルゴリズムの擬似コードを議論しました。我々は貪欲な選択が安全な手段であることを証明し、最後にこの解決策を示すためにC++のプログラムを作成しました。この概念の全体的な時間計算量はO(Nlog2N)です。では今日はここまでです。ご覧いただきありがとうございました。

さらに読む

もしナップサック問題や他のグリーディ法についてもっと学びたいなら、以下のウェブサイトを参照してみてください。

以下のウェブサイトにある「貪欲アルゴリズム」の内容を日本語で要約すると、次のようになります。

ナップザック問題（ナップザックもんだい）は、組み合わせ最適化問題の一種であり、物品の組み合わせを最適化する問題です。与えられた重みと価値を持つ物品を、制約を満たしつつ、ナップザックに入れる方法を探求します。この問題は計算機科学や経済学、数学などの分野で広く応用されています。