A Binary Tree with a minimum heap structure.
A Min Heap Binary Tree refers to a type of Binary Tree where the root node has the smallest key value among all nodes in the tree.
The Min Heap property is applicable to all sub-trees in the tree, as stated in the definition above.
With the exception of the last 2 layers, almost all nodes, except for the final 2 layers, should possess two offspring. Essentially, this resembles a nearly complete binary tree.
The tree shown below exemplifies a binary tree of minimum heap type, as it complies with the aforementioned two conditions.
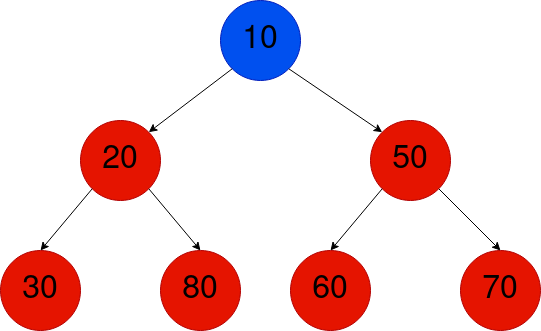
After discussing the concept of a min heap tree, let’s examine the methods of representing it.
A Min Heap Tree‘s depiction.
The commonly used format to index a Min Heap Binary Tree is an array representation.
| Current Node | arr[i] |
| Parent Node | arr[(i-1)/2] |
| Left Child | arr[(2*i) + 1] |
| Right Child | arr[(2*i )+ 2] |
The base of the entire tree can be found at arr[0].
The pattern in the table above can easily be identified by referring to the indexing displayed in the figure below.
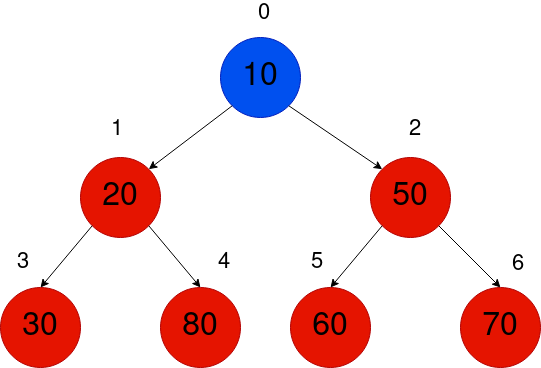
A Binary Heap array is essentially a Binary Tree that is indexed using a Level Order Traversal.
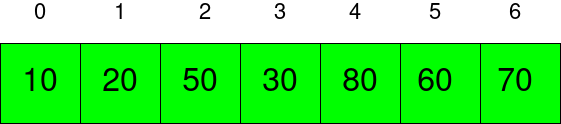
The Min Heap Tree is represented in the figure above with an array.
Now that we’ve discussed the ideas, let’s proceed with putting this into practice using C!
Executing a Min Heap Tree
To construct the Min Heap, we will utilize the array representation. Initially, let us begin creating the Min Heap structure.
typedef struct MinHeap MinHeap;
struct MinHeap {
int* arr;
// Current Size of the Heap
int size;
// Maximum capacity of the heap
int capacity;
};
As elements are inserted or deleted, the array of elements will have its size updated.
The array has a maximum size known as its capacity.
We have to write certain functions to indicate that we are representing a Min Heap Tree, such as locating the parent and the children.
int parent(int i) {
// Get the index of the parent
return (i - 1) / 2;
}
int left_child(int i) {
return (2*i + 1);
}
int right_child(int i) {
return (2*i + 2);
}
int get_min(MinHeap* heap) {
// Return the root node element,
// since that's the minimum, by the min-heap
// property
return heap->arr[0];
}
We will create functions that are responsible for initializing and deallocating the heap.
MinHeap* init_minheap(int capacity) {
MinHeap* minheap = (MinHeap*) calloc (1, sizeof(MinHeap));
minheap->arr = (int*) calloc (capacity, sizeof(int));
minheap->capacity = capacity;
minheap->size = 0;
return minheap;
}
void free_minheap(MinHeap* heap) {
if (!heap)
return;
free(heap->arr);
free(heap);
}
Now that we have that covered, let’s proceed to learn how we can add elements.
Adding elements to the Min Heap.
The algorithm for inserting an element into the tree is straightforward.
Analyzing the algorithm step by step.
- First, always insert at the bottom of the tree. The initial position of the inserted element is at the last level.
- We will now need to update the position of this element so that the min-heap property is satisfied.
- Since the root node of every sub-tree must be the minimum, check the sub-tree of its immediate parent.
- If the parent is greater than this inserted element, we need to update its position by swapping it.
- But we are not yet done, since the min-heap property may be violated of the updated node’s sub-tree!
- We need to keep swapping until we reach the root node, after which we are done.
To grasp this method, let’s consider an instance.
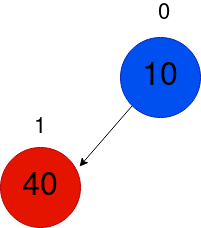
Please contemplate the tree illustrated beneath, consisting solely of a singular component.

We can add the number 40. As there is only one element, it will be inserted at the bottom. We can see that the min-heap condition is met since 10 is smaller than 40. Hence, no swapping is required.
Afterward, we will input 50. A comparable method ensues.
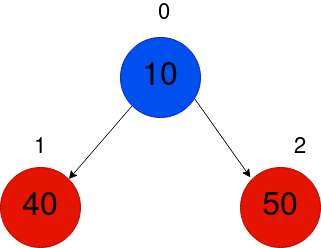
Afterwards, we will add the number 5. Hence, our initial insertion will be at index 3, positioned at the bottom of the tree.
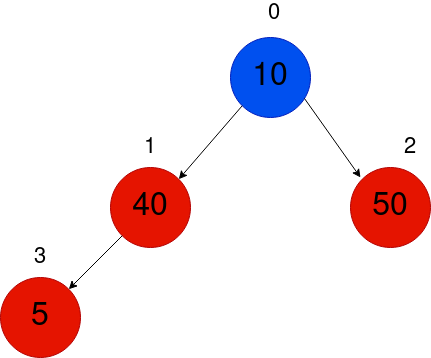
Once the sub-tree 1-3 fails to satisfy the min heap property, the whole tree is affected. Consequently, we are required to continuously exchange the element with its parent until the root is reached.
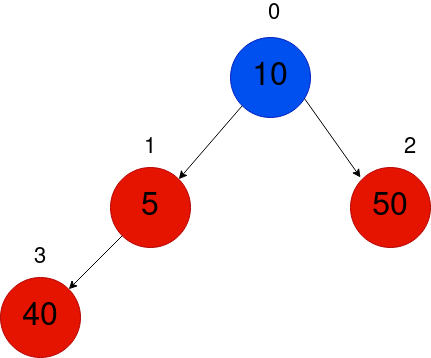
In order to maintain the min-heap property for the sub-tree rooted at node 0, we require another swap.
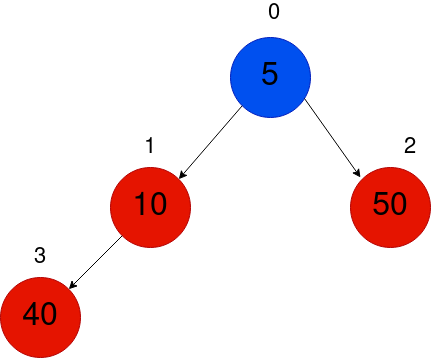
Okay. Now that we have seen it, let’s put it into writing!
MinHeap* insert_minheap(MinHeap* heap, int element) {
// Inserts an element to the min heap
// We first add it to the bottom (last level)
// of the tree, and keep swapping with it's parent
// if it is lesser than it. We keep doing that until
// we reach the root node. So, we will have inserted the
// element in it's proper position to preserve the min heap property
if (heap->size == heap->capacity) {
fprintf(stderr, "Cannot insert %d. Heap is already full!\n", element);
return heap;
}
// We can add it. Increase the size and add it to the end
heap->size++;
heap->arr[heap->size - 1] = element;
// Keep swapping until we reach the root
int curr = heap->size - 1;
// As long as you aren't in the root node, and while the
// parent of the last element is greater than it
while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
// Swap
int temp = heap->arr[parent(curr)];
heap->arr[parent(curr)] = heap->arr[curr];
heap->arr[curr] = temp;
// Update the current index of element
curr = parent(curr);
}
return heap;
}
Next, we will proceed with the implementation of the deletion procedure.
Remove from the Minimum Heap
Firstly, let’s focus on deleting the root element as the root is closely linked to the min-heap structure, before discussing the deletion of an element at any given index.
In order to remove the smallest element (the root), we will proceed as follows:
- Update the root as the last element of the array (tree)
- We will now remove the last element at the bottom. This is similar to swapping and deleting at the end! Only because we don’t care about the root value anymore, we simply update it instead.
- The problem again is that we need to maintain the min-heap property.
- So we must ensure that the whole tree maintains this property. We will use a function called heapify() to do this for us.
After performing the heapify() method, the deletion process will be fully executed.
MinHeap* delete_minimum(MinHeap* heap) {
// Deletes the minimum element, at the root
if (!heap || heap->size == 0)
return heap;
int size = heap->size;
int last_element = heap->arr[size-1];
// Update root value with the last element
heap->arr[0] = last_element;
// Now remove the last element, by decreasing the size
heap->size--;
size--;
// We need to call heapify(), to maintain the min-heap
// property
heap = heapify(heap, 0);
return heap;
}
The process of heapify()
This function receives an index called “index” and ensures the min heap property remains intact by swapping it with the smallest element within its immediate subtree.
The tree that is produced will adhere to the min-heap condition.
This includes locating the sub-tree’s smallest element and exchanging it with the current element.
Once this is done, we must ensure that the entire tree meets this requirement as well. Therefore, we must repeatedly invoke the procedure on the smallest element until we reach the root.
MinHeap* heapify(MinHeap* heap, int index) {
// Rearranges the heap as to maintain
// the min-heap property
if (heap->size <= 1)
return heap;
int left = left_child(index);
int right = right_child(index);
// Variable to get the smallest element of the subtree
// of an element an index
int smallest = index;
// If the left child is smaller than this element, it is
// the smallest
if (left < heap->size && heap->arr[left] < heap->arr[index])
smallest = left;
// Similarly for the right, but we are updating the smallest element
// so that it will definitely give the least element of the subtree
if (right < heap->size && heap->arr[right] < heap->arr[smallest])
smallest = right;
// Now if the current element is not the smallest,
// swap with the current element. The min heap property
// is now satisfied for this subtree. We now need to
// recursively keep doing this until we reach the root node,
// the point at which there will be no change!
if (smallest != index)
{
int temp = heap->arr[index];
heap->arr[index] = heap->arr[smallest];
heap->arr[smallest] = temp;
heap = heapify(heap, smallest);
}
return heap;
}
We are capable of enhancing the delete_minimum() function to remove any element.
Removing any random element
To achieve this, simply assign the desired element the minimum feasible value, which is obtained by subtracting 1 from get_min(). The reason being that the value must be lower than the current minimum.
Now, we will continue exchanging elements until we update the position in order for the new root to be this particular element.
We have returned to our original delete_minimum() function, where we can effortlessly remove the new root.
This will be the complete procedure for deleting.
MinHeap* delete_element(MinHeap* heap, int index) {
// Deletes an element, indexed by index
// Ensure that it's lesser than the current root
heap->arr[index] = get_min(heap) - 1;
// Now keep swapping, until we update the tree
int curr = index;
while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
int temp = heap->arr[parent(curr)];
heap->arr[parent(curr)] = heap->arr[curr];
heap->arr[curr] = temp;
curr = parent(curr);
}
// Now simply delete the minimum element
heap = delete_minimum(heap);
return heap;
}
Finally, we’re finished. Now, I’ll display the complete code thus far, including the print() function, to allow you to visualize the tree.
The entire code
#include <stdio.h>
#include <stdlib.h>
typedef struct MinHeap MinHeap;
struct MinHeap {
int* arr;
// Current Size of the Heap
int size;
// Maximum capacity of the heap
int capacity;
};
int parent(int i) {
// Get the index of the parent
return (i - 1) / 2;
}
int left_child(int i) {
return (2*i + 1);
}
int right_child(int i) {
return (2*i + 2);
}
int get_min(MinHeap* heap) {
// Return the root node element,
// since that's the minimum
return heap->arr[0];
}
MinHeap* init_minheap(int capacity) {
MinHeap* minheap = (MinHeap*) calloc (1, sizeof(MinHeap));
minheap->arr = (int*) calloc (capacity, sizeof(int));
minheap->capacity = capacity;
minheap->size = 0;
return minheap;
}
MinHeap* insert_minheap(MinHeap* heap, int element) {
// Inserts an element to the min heap
// We first add it to the bottom (last level)
// of the tree, and keep swapping with it's parent
// if it is lesser than it. We keep doing that until
// we reach the root node. So, we will have inserted the
// element in it's proper position to preserve the min heap property
if (heap->size == heap->capacity) {
fprintf(stderr, "Cannot insert %d. Heap is already full!\n", element);
return heap;
}
// We can add it. Increase the size and add it to the end
heap->size++;
heap->arr[heap->size - 1] = element;
// Keep swapping until we reach the root
int curr = heap->size - 1;
// As long as you aren't in the root node, and while the
// parent of the last element is greater than it
while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
// Swap
int temp = heap->arr[parent(curr)];
heap->arr[parent(curr)] = heap->arr[curr];
heap->arr[curr] = temp;
// Update the current index of element
curr = parent(curr);
}
return heap;
}
MinHeap* heapify(MinHeap* heap, int index) {
// Rearranges the heap as to maintain
// the min-heap property
if (heap->size <= 1)
return heap;
int left = left_child(index);
int right = right_child(index);
// Variable to get the smallest element of the subtree
// of an element an index
int smallest = index;
// If the left child is smaller than this element, it is
// the smallest
if (left < heap->size && heap->arr[left] < heap->arr[index])
smallest = left;
// Similarly for the right, but we are updating the smallest element
// so that it will definitely give the least element of the subtree
if (right < heap->size && heap->arr[right] < heap->arr[smallest])
smallest = right;
// Now if the current element is not the smallest,
// swap with the current element. The min heap property
// is now satisfied for this subtree. We now need to
// recursively keep doing this until we reach the root node,
// the point at which there will be no change!
if (smallest != index)
{
int temp = heap->arr[index];
heap->arr[index] = heap->arr[smallest];
heap->arr[smallest] = temp;
heap = heapify(heap, smallest);
}
return heap;
}
MinHeap* delete_minimum(MinHeap* heap) {
// Deletes the minimum element, at the root
if (!heap || heap->size == 0)
return heap;
int size = heap->size;
int last_element = heap->arr[size-1];
// Update root value with the last element
heap->arr[0] = last_element;
// Now remove the last element, by decreasing the size
heap->size--;
size--;
// We need to call heapify(), to maintain the min-heap
// property
heap = heapify(heap, 0);
return heap;
}
MinHeap* delete_element(MinHeap* heap, int index) {
// Deletes an element, indexed by index
// Ensure that it's lesser than the current root
heap->arr[index] = get_min(heap) - 1;
// Now keep swapping, until we update the tree
int curr = index;
while (curr > 0 && heap->arr[parent(curr)] > heap->arr[curr]) {
int temp = heap->arr[parent(curr)];
heap->arr[parent(curr)] = heap->arr[curr];
heap->arr[curr] = temp;
curr = parent(curr);
}
// Now simply delete the minimum element
heap = delete_minimum(heap);
return heap;
}
void print_heap(MinHeap* heap) {
// Simply print the array. This is an
// inorder traversal of the tree
printf("Min Heap:\n");
for (int i=0; i<heap->size; i++) {
printf("%d -> ", heap->arr[i]);
}
printf("\n");
}
void free_minheap(MinHeap* heap) {
if (!heap)
return;
free(heap->arr);
free(heap);
}
int main() {
// Capacity of 10 elements
MinHeap* heap = init_minheap(10);
insert_minheap(heap, 40);
insert_minheap(heap, 50);
insert_minheap(heap, 5);
print_heap(heap);
// Delete the heap->arr[1] (50)
delete_element(heap, 1);
print_heap(heap);
free_minheap(heap);
return 0;
}
Result
Min Heap:
5 -> 50 -> 40 ->
Min Heap:
5 -> 40 ->
The time complexity of the implementation.
Below, we have stated the time complexities of the procedures mentioned above.
| Function | Time Complexity |
get_min() |
O(1) |
insert_minheap() |
O(logN) |
delete_minimum() |
Same as insert – O(logN) |
heapify() |
O(logN) |
delete_element() |
O(logN) |
Get the Code
I have uploaded the complete code as a Github Gist, which you can download. If you have any questions, feel free to ask them in the comment section below!
In conclusion, summarizing the above information.
In this article, we discovered the ways to depict a Binary Tree of Min Heap and examined its execution in the C language.
One possible paraphrase of “References” would be “Citations” or “Sources”.
- An illustration of Heaps, from Cormen
- Wikipedia article on Binary Heaps
More tutorials
jQuery parent() and children() tree traversal functions(Opens in a new browser tab)
How to Delete Elements from an Array in Java(Opens in a new browser tab)
How to include items to a list in Python(Opens in a new browser tab)
convert string to character array in Java.(Opens in a new browser tab)
Creating a GraphQL API using Prisma on Silicon Cloud’s App Platform(Opens in a new browser tab)

